【都立自校作成数学問題】二次関数と多角形の面積

こんにちは。鈴木です。

この記事では、前の記事に続き、新宿高校の平成29年度の問題について書きます。

前の記事とはこちらです。

https://sugaku1bann.com/2022/03/17/sinnjukujikousaku/

今回は、二次関数です。

問題がこちらです。

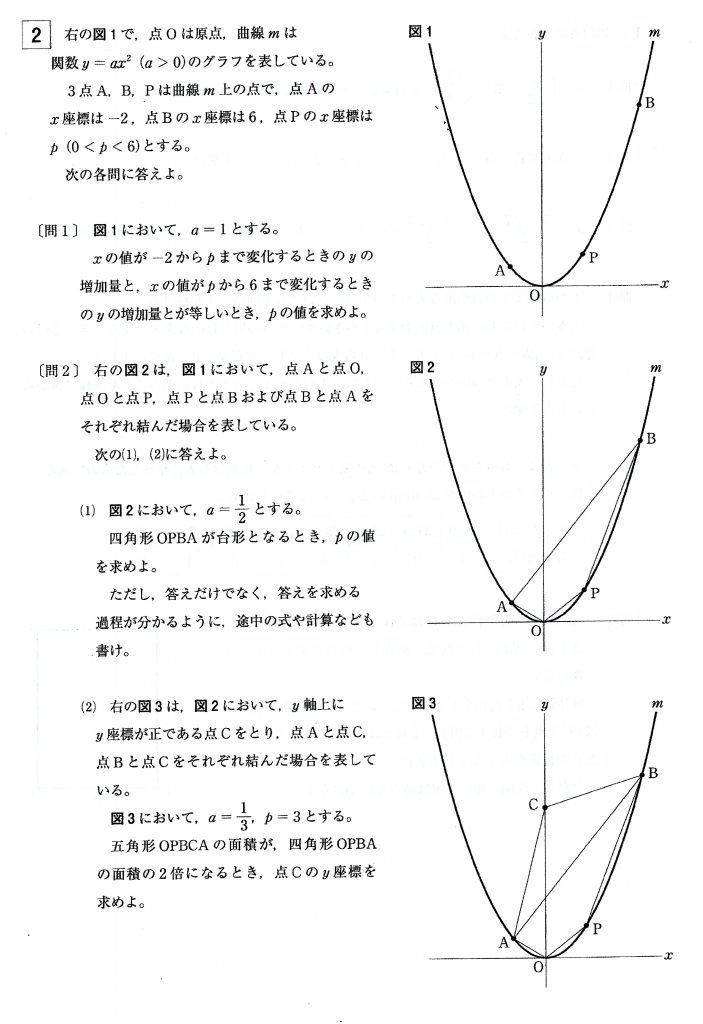
増加量とは何かを今一度チェックすべし！

まずは根本的に、何が問われているのかを、正確に把握しましょう。

この問題では、pの値を求めましょうとあります。

どんなときの、pの値でしょうか。

xの値が、－2からpまで変化するときのyの増加量と、xの値がpから6まで変化するときのyの増加量とが、等しくなるときのpの値ですね。

それでは、まず初めに考えるべきこと

それは、増加量をどう出すのか、ということです。

○○から✖✖まで変化するときのyの増加量

例えば、xの値が1から3まで変化するときのyの増加量を求めなさいと言われて、x=1のときy=5、x=3のときy=2になったとき、本当に多くある間違いが

yの増加量=5－2=3

としてしまうことです。

何やら生徒さんは、増加だから、多い方から少ない方を引くと思っていることがあるのですが、ここで大事な考え方は、減ることも増加のうちであるということです。

この例の場合であったら、本当は、2－5=－3としなければいけません。

つまり、xの値が○○から✖✖まで変化する

と言われたら

xの値が(✖✖)のときのyの値から、xの値が(○○)のときのyの値を引く

ということを、覚えておかなければいけません。

このことを肝に命じて、式を立てていきましょう。

「台形となる」とはどういうことか？

問い2の(1)は、四角形OPBAが台形になるとありますが、どんな台形になるのかが分かることが大事です。

台形とは、どんな形ですか？

とある四角形において、1組の対辺が平行であれば、その四角形は台形になってくれるのですが、この問題の場合は、どの辺同士が平行になってくれれば良いのでしょうか。

この場合は、辺OPと辺ABが平行になってくれれば良いのです。

そして、そもそも今求めなければいけないものは何かというと、pの値でしたね。

辺OPと辺ABが平行になるとき、これはつまり、何かが一致すれば良いわけですが、何が一致すれば良いのか。

それは、直線OPと直線ABの傾きが一致すれば良いわけです。

まずは、直線ABの傾きを求めてから、直線OPの傾きをpで表して、pについての方程式を立てましょう。

座標を求めるときは文字で置こう！

(2)は点Cの座標を求めなさいとあるのですが、高校受験の関数の問題を見ていると、最後の問題は決まって、どこかの座標を求めさせる問題がほとんどです。

このとき、大事な考え方は何かというと

座標を文字で置いて、そのあとに方程式を立てて解く

という、高校で学ぶ数学にも通じる考え方です。

とは言ったものの、この問題は五角形の面積などという、一見、かなり難しそうなことをやるわけですが、ここでも大事な考え方が出てきます。

図形は分割して面積を求める

問い2の(2)においては、a=1/3、p=3と出ているので、3点P、A、Bの座標は、もう決まってしまいます。

すると必然的に、四角形OPBAの面積は決まるのですが、その求め方が問題ですね。

みなさんなら、どうやって求めますか？

どうやって、図形を分割しますか？

図形を分割すると書きましたが、いろいろ考えているうちに、全体の図形の面積から、一部の図形の面積を引く方法でもできることに気付いたので、ぜひ、自分で答を出してみて下さい。

解答は、最後に載せます。

C(0,c)と置いて方程式を作る

前の話に戻って、点Cの座標を(0,c)とでも置きましょう。

これまでのことを整理しておくと

①3点P、A、Bの座標が分かっている

②四角形OPBAの面積が分かる

③点Cの座標を(0,c)と置いて、方程式を作る

ということなのですが、③の、方程式を作る、ということについて、もう少し詳しく見ていきましょう。

まずは、直線ABの方程式を求めましょう。

直線ABの方程式が求まったら、直線ABとy軸との切片が分かるので、この点をDとしましょう。

すると、三角形ABCの面積を求めるときに、三角形ACDと三角形BCDに分割して求めることができるわけです。

このとき、どちらの三角形においても、辺CDを底辺と見ることができますが、実は辺CDの長さが、cを使って表現されるわけです。

すると、三角形ABCの面積も、cを使った式として表現されるのですが、このときできた式が、何に等しくなれば良いのか。

四角形OPBAと等しくなれば良いのです。

この理由が分からないという人は、もう一度、問題文を読んでみて下さい。

あぁ、そういうことか、となるはずです。

この記事のまとめ

ということで、解答がこちらです。

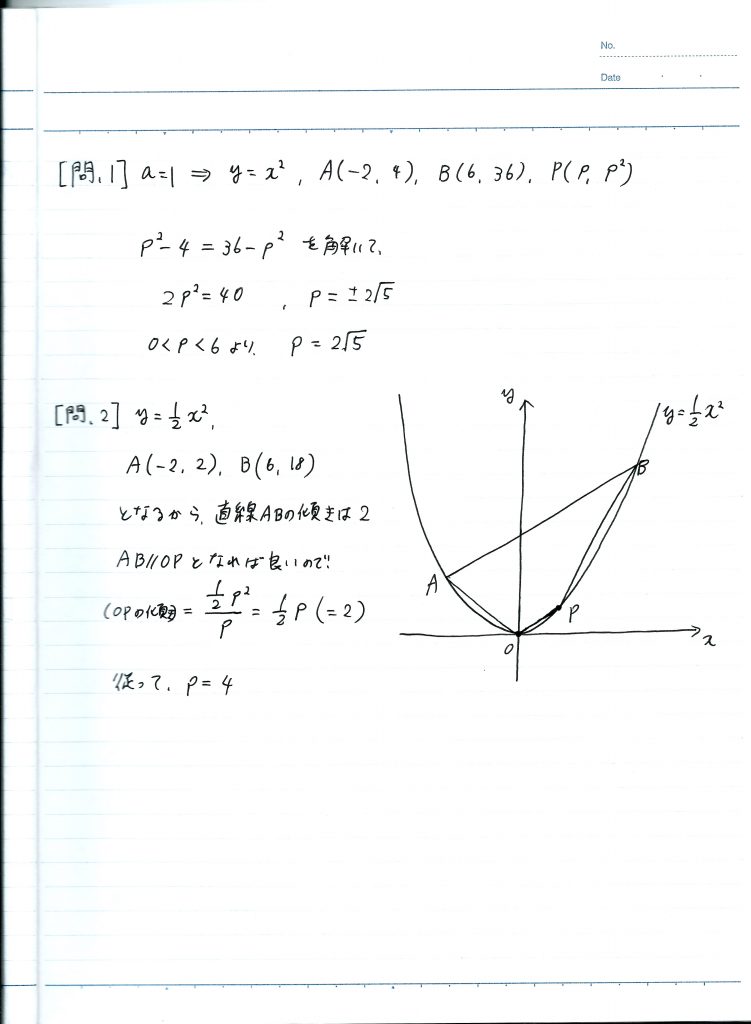
高校入試の関数の問題では

・変化の割合の計算方法

・図形(特に三角形）の面積の出し方

・座標を求めるタイプの問題

に慣れておくことが大事です。

日頃から自分で図やグラフを描いて、問題演習に取り組んで下さいね。