こんにちは。世田谷区のプロ家庭教師、数学専門の鈴木です。
今回は、三角形の角度や証明問題についてです。
以下の記事で、2次関数の問題も解説しております。
https://sugaku1bann.com/2022/03/17/sinnjukujikousaku2/
最後に面積比など、難しく感じる問題も出てきますが、何度もお伝えしている通り、この考え方があるから、問題が解ける!という部分に注意して書いていきますので、楽しみにしていて下さいね。
角度は分かるところから攻める!
問題がこちらです。

問題を見ると、二等辺三角形の問題ですね。
ここでは、二等辺三角形についての性質を理解できているかどうかが鍵となります。
∠ADBは何度か?
問題文を読むと、辺BCの中点がDとなっていますね。
頂点Aと点Dとを結んだ線分は、辺BCとどんな風に交わるのか?
知っている人も多いかと思いますが、線分ADと辺BCは、垂直に交わります。
∠ADB=90度となります。
問題は、ここからどう考えていくのか、ということですが、こうした角度の問題を解くときは、以下のことを常に意識しておいて下さいね。
三角形の内角の和を意識する
三角形の内角の和、もちろん180度ですが、どの三角形に適用させていけば、答が求められそうですか?
問題文では、∠BQD=aとしなさいとありますね。
今、∠ADB=90度であることが分かっています。
すると、これらの角度はそれぞれ、三角形BQDの中に含まれているので・・・
そうです。
∠QBDの大きさが、aを用いて求められるのです。
それが分かったら、今度はどこの角度が分かりそうですか?
問い1では、CB=CPを仮定していますね。
実際の授業では、こんなやりとりをして、生徒さんは、答の求め方に気付いてくれそうです。
先生「CB=CPということは、三角形BCPは、どんな三角形になっているか分かるかな?」
生徒「そうですね・・・、あ、二等辺三角形になっていますね」
先生「そうだね。二等辺三角形ということは、この場合、どことどこの角度が等しくなっている?」
生徒「CB=CPだから、∠CBPと∠CPBが同じになっています」
先生「そうそう。この2つが今、文字aで表わされているから、今度は∠PCBも、aで表してごらん」
生徒「・・・できました。三角形ABCは二等辺三角形だから、∠PCB=∠ABCなので、∠ABCから∠PBCを引けば、答が出るんですね」
先生「その通りだね。最後まで、答を出してみましょう!」
といった具合に、この問題は、ひたすら二等辺三角形に注目して解いていく問題であることが分かります。
相似と面積比の問題
問い2は問題文に書いてあることを、ただ読み流すだけではなく、文として書いてあることと、図2において示されていることが、果たして一致しているのかどうかを、自分で確かめながら読んでみて下さい。
(1)は証明問題ですが、相似であることを示す問題ですね。
相似条件を3つ覚えていることはもちろん、図を見て、問題文を読んで、どれが使えそうなのかをすぐに判断する力を、日頃の勉強では身につけていきましょう。
この問題では、(1)はひとまず、辺の比については何も述べていないので、もう、使う条件は限られています。
(2)は、少し難しい
かくいう私も、中学生の頃は、(2)みたいな問題は、あまり得意ではありませんでした。
その理由は
・図が与えられただけでは、何から考えて良いのか分からない
・説明されても、「何でそう考えるのか?」というポイントが分かりずらい
・結局「図形はセンス!」の一言で済まされてしまうことが多い
などなど、特に、図形の問題を解くには、何かしらのセンスが求められているものだと、信じて疑わなかったわけです。
しかし、断言します。
いくら難しい問題であるとはいえ、特に図形の問題の場合は、一定の考え方のパターンは存在する
ということです。
具体的には、以下の通りです。
ひたすら相似な図形を探す
まず、何から考えれば良いのか、ということですが、それはこの、相似な図形を探すことがまずは第一です。
なぜかというと、この問題ではそもそも、面積の比を知りたいわけですので、線分の比が分かることが、大きな手がかりになり得るからです。
ここでは直角も関係してくるので、三平方の定理を使って、具体的に線分の長さを求めることもできます。
線分AQと線分FQの比を求めたい!
三角形AQPと三角形BFQを見ると、それぞれ線分AQと線分FQを底辺と見れば良さそうです。
その根拠は、実はこの2つの三角形は既に、これらの線分を底辺と見ると、高さが分かってしまうからです。
三角形AQPの高さは1、三角形BFQの高さは2という結論だけ書いておくので、理由を考えてみて下さい。面白いかと思います。
さて、こんな情報まで分かってきたところで、具体的に、相似な図形を探していきましょう。
線分AQと線分FQの比が知りたいので、それらの線分を含む三角形たちについて、相似になるもの同士を探してみて下さい。
この考えでいくと、まず見つかるのは
三角形APH∽三角形ADC
です。
点Pは辺ACの中点であることから、線分APの長さが分かり、三平方の定理で、線分ADの長さも分かることから
AP:AH=AD:AC
と式を立てれば、線分AHの長さが分かります。
目的は、線分AQと線分FQの比を求めることなのですが、ここからやるべきことを先に書いておくと
①三角形BDFと三角形ADCの相似に注目して、線分DFの長さを求める
②線分PHの長さと線分BFの長さが具体的に分かるから、これらの線分比を出すことで、結局HQ:FQが分かる
③HF=AD-(AH+DF)だから、線分HFの長さが分かれば、②の結果を使って、線分HQと線分FQの長さも分かる
これで、AQ:FQが分かるので、全体として、三角形AQPの面積と三角形BFQの面積の比が分かるというわけです。
この記事のまとめ
少し長くなってしまいましたが、解答がこちらです。
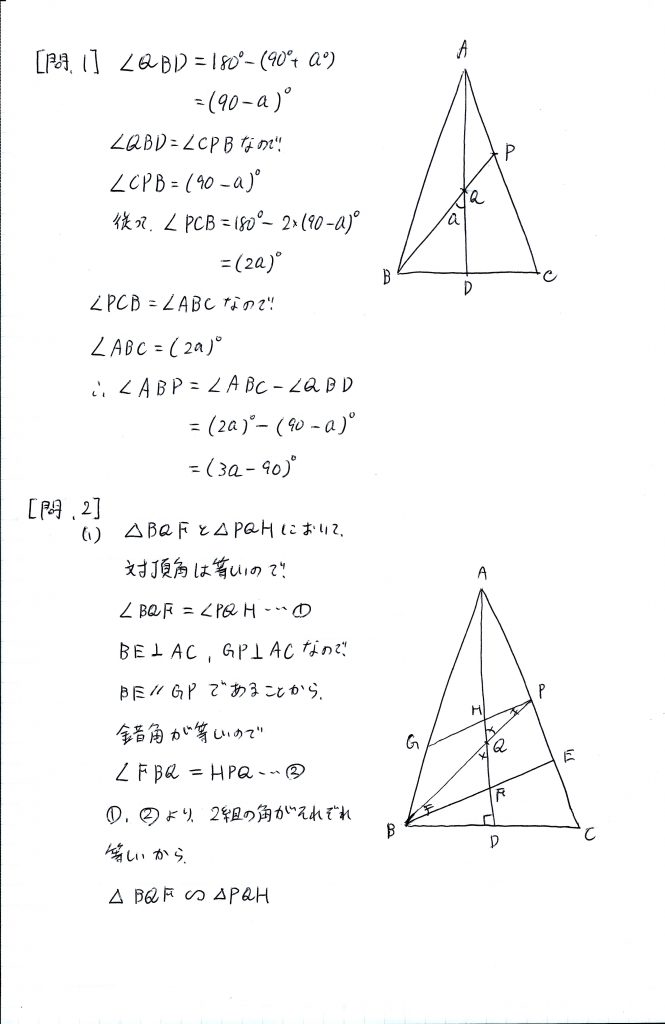
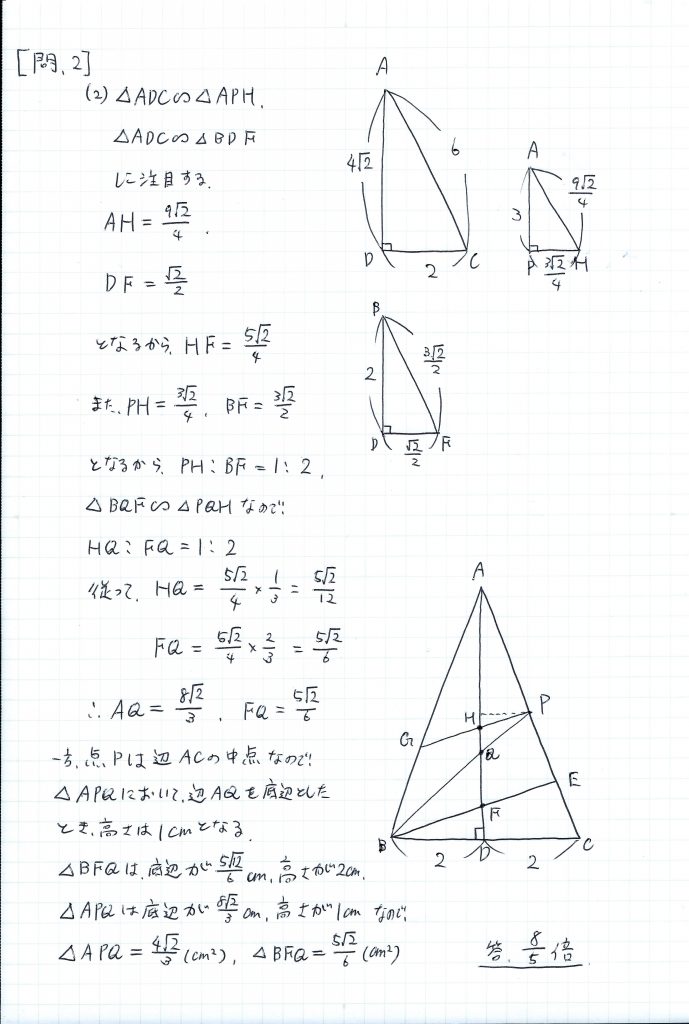
図形の問題を解くときは
・角度を求めるときは、論理の飛躍なしに、分かるところから求めていく
・自分で、相似になる図形を探してみる
・面積の比を求めるときは、まずは線分の比から考えてみる
・直角が関係する場合、三平方の定理もどんどん使う
・問題用紙に載っている図だけではなく、自分で分かりやすい図を余白に書き直して、そこに分かっていることを書き込む
など、解くためには色んな工夫ができると思います。