こんにちは。算数・数学専門のプロ家庭教師の鈴木です。
今日は女子学院中学の、2022年の算数入試問題のうち、大問4の解説をしていきたいと思います。
大問4は、立体の展開図に関する問題ですが、「具体例から推測する力」が重要になってきます。
はじめの問題がこちらです。
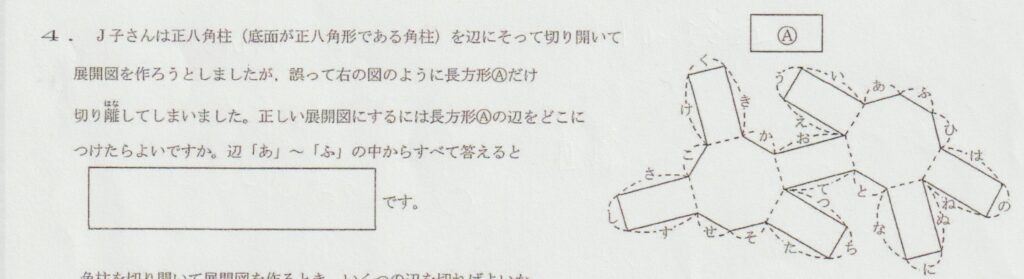
「すべて答える」に気をつける
この問題の場合、展開図を普段から自分で描いているような人であれば、「お」が「え」にくっつき、「う」が「か」にくっつき、「い」が「き」にくっつき・・・、
と考えて、組み立てたところを図にすると、「ふ、け、さ、こ」とくっつくところがないことが分かります。
「すべて答える」とあるので、答の書き忘れや書き間違い、辺の見間違いがないかどうかを、目で見て確かめられると、ミスなく答えることができます。
次の問題がこちらです。
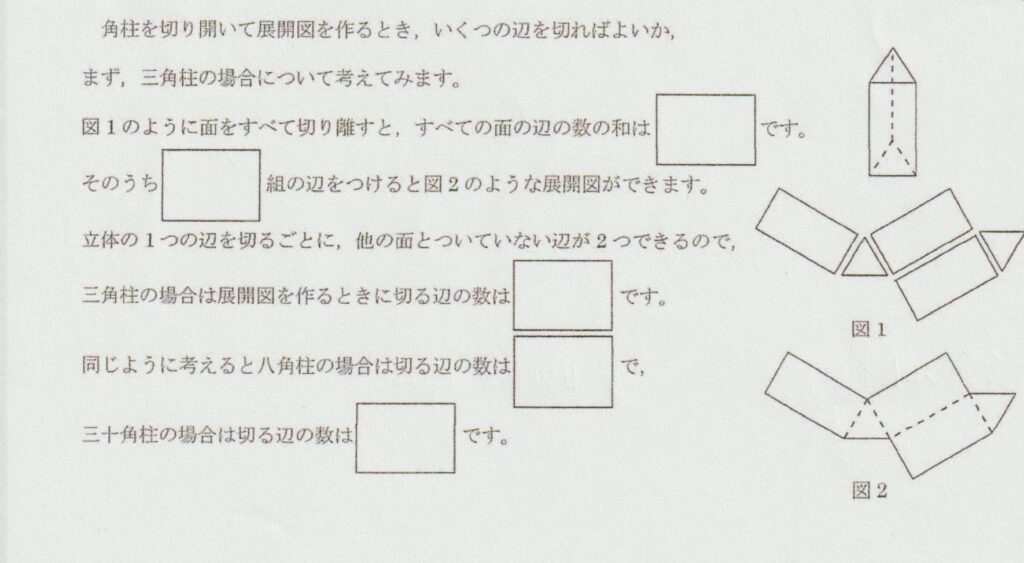
「何をしようとしているのか」をまずは把握して、面や辺を数える
「いくつの辺を切ればよいか」とありますよね。
ここでは立体の展開図を作るとき、はじめの問題のように「切れてしまった面がでないように、展開図を作りたい」と問題文を読み取れると、なぜこのような問題になっているのかが分かります。
問題文を読み進めていくと、三角柱の場合には図1のように面をすべて切り離すと、すべての面の辺の数の和は4×3+3×2で18となりますよね。
次に、図2のようにするためには、図から4組の辺をくっつけてあげれば良いことが分かります。
これらを踏まえた上で、「切れてしまった面がでないように展開図を作る」ためにどう考えれば良いかを、式として表現します。
三角柱の場合は、「すべて切り離したときにできる面の辺の数」-「くっついた辺の数」を計算すると、「くっついた辺の数」は、「くっついたのは4組の辺」であることから、「2×4」で8であることが分かり、「切れてしまった面がでない展開図」には、10個の辺があります。
ところが、問題では「切る辺の数」を聞かれていますよね。
角柱の辺を一つ切るごとに、2つの辺が表れることになるので、切る辺の数は「展開図にある辺の数」÷2で求まります。
このような考え方と「同じように考える」と、八角柱の場合には、以下の式によって、答えが出ます。
八角柱の場合に切る辺の数
「すべて切り離したときにできる面の辺の数」-「くっついた辺の数」=8×2+4×8-2×9=30
「展開図にある辺の数」÷2=30÷2=15
同じく三十角柱の場合に切る辺の数
「すべて切り離したときにできる面の辺の数」-「くっついた辺の数」=30×2+4×30-2×31=118
「展開図にある辺の数」÷2=118÷2=59
このような問題をできるようにするための対策
展開図の問題では、必ず「組み立ててみたところ」を、普段から描くようにすると良いですね。
そうすることで、「どの辺とどの辺がくっつくのか」を、すぐに考えられるようになります。
また、この問題は「解き方を覚える」という考えが通用しないような、最も分かりやすい一例です。
問題を見て、「このような具体例から、こんなことが言える」と推測して、それが正しいことを確かめられるような勉強の仕方が、ここで紹介したような問題を解く際に、役に立ちます。
そうした勉強の仕方は、主に「整数の問題、規則性の問題」を学ぶことで身につきますので、難しい問題よりも、基本的な問題を練習していく中で習得できると良いと思います。
