こんにちは。算数・数学専門家庭教師の鈴木です。
今回は東京大学大学院の院試の解答を載せておきますね。
算数から大学院の入試まで、数学に関する全ての指導が可能ですので、ご相談がある方はいつでもお問合わせ下さいませ。
令和4年度の院試のうち、微積分の基礎に関する問題がこちらです。

まずは積分する領域を図示

重積分の計算をするときは、必ず領域を図示しましょう。
そうすることで、積分の順序の変更などに気付くことができます。
次に極座標へと変換

円形の領域が出てくるので、迷いなく極座標に変換しましょう。
図示した白色の領域については、rとθの関係がどのようになるのか、同じような問題を解いたことがある方はすぐに分かると思います。

三角関数の有理関数は次数を下げて!

cosの2乗が出てきて、しかも有理関数になっているので、当初私は「積分できるのか?」とも思いましたが、次数を下げるとうまくいく気がしました。
タンジェントの半角による変数変換を使う

三角関数の、しかも有理関数の積分で「tan(u/2)」などとおくのは、よく知られた置換の仕方ですよね。
「次数を下げる」「よくある置換を使う」という何気ない方法で、積分ができてしまうのですね。
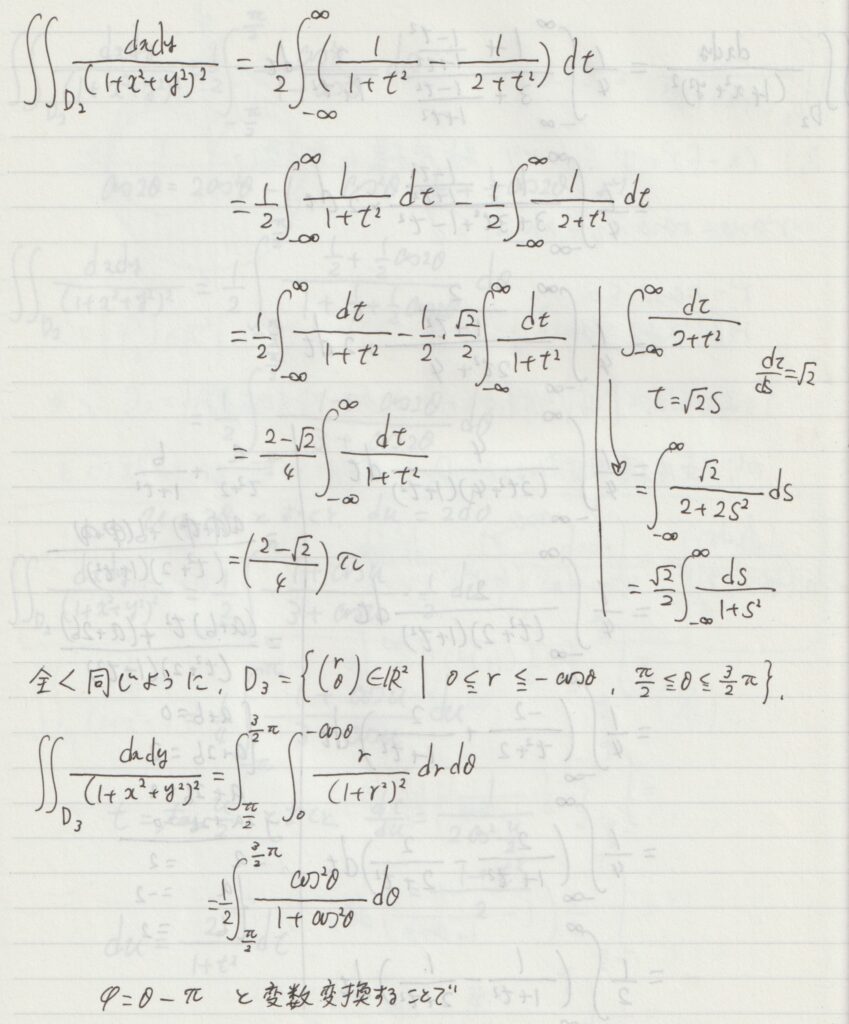
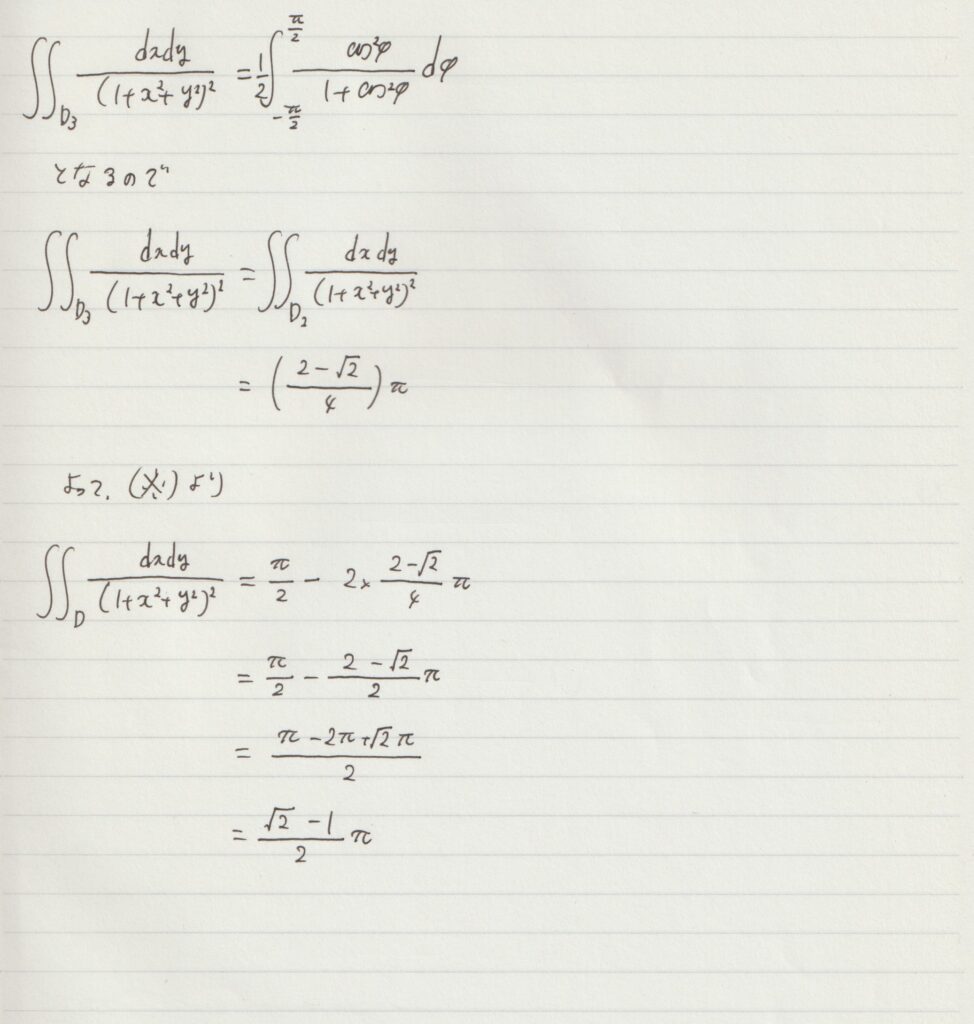
よくある積分計算のまとめ
この問題に限らず、どこの大学院の院試でも重積分の計算はよく出てきます。
というより、院試を受ける以上必須ですね。
「極座標を使う」「三角関数と有理関数の積分」の他にも、「重積分の収束」に関する問題などが、大学院の (しかも数学・数理科学系の) 院試ではよく問われます。
積分の計算が苦手という方は、まず、極座標のような「典型的な変数変換」からできるようにしていけると良いと思います。
