こんにちは。算数・数学専門家庭教師の鈴木です。
今日は2022年度の日比谷高校の数学入試問題について解説していきます。
その中でも今回は大問3番について解説します。
↓問題がこちら↓


【問1のポイント】大事なのは円周角と中心角・弧の長さの比
問1は角度の問題ですが、主に円周角と中心角の関係を使って角度を出します。
問1では出てきませんでしたが、同じ半径の円であれば「弧の長さの比は中心角の比と一致する」という知識も必須です。
これらの知識を前提として「角度の問題は分かるところから値を出す」という気持ちを持って正解を出すことが大事です。
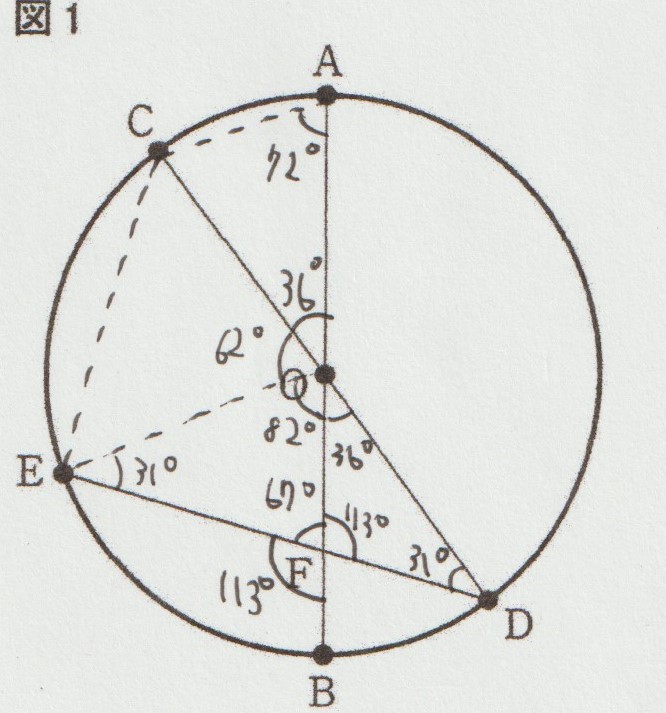
上の図のように、まず分かることは∠AOC=36°、またそこから分かることは∠DOB=36°、∠OFE=67°、∠OFD=113°となることなどが分かります。
そうすると∠ODF=31°も分かりますが、∠ODFは弧CEに対する円周角なので、弧CEに対する中心角である∠COE=62°となることも分かります。
すると∠EOB=82°となることも分かりますが、そのとなりの∠DOF=36°なので、∠EOD=118°となります。
∠EODは弧EDに対する中心角なので、この弧に対する円周角である∠DCEとの間には「∠DCEの2倍が∠EOD」という関係が成り立ちます。
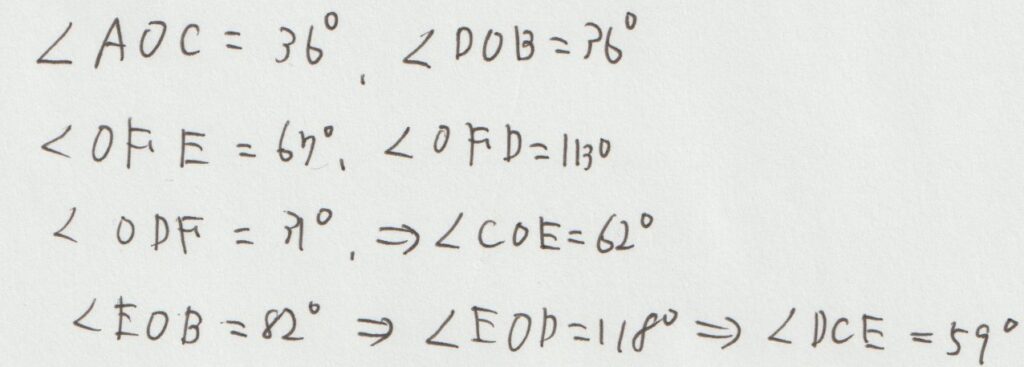
【問2のポイント】相似を示してから合同を示す
難関都立の問題ではよくあるのですが、2組の三角形の合同を示す段階において「まず他の三角形の合同や相似を示してから題意を示す」というタイプの問題があります。
この問題がまさにそうだったのですが、まずは下の図を見て、どのように△OGJ≡△DHKを示せば良いか、考えてみて下さい。
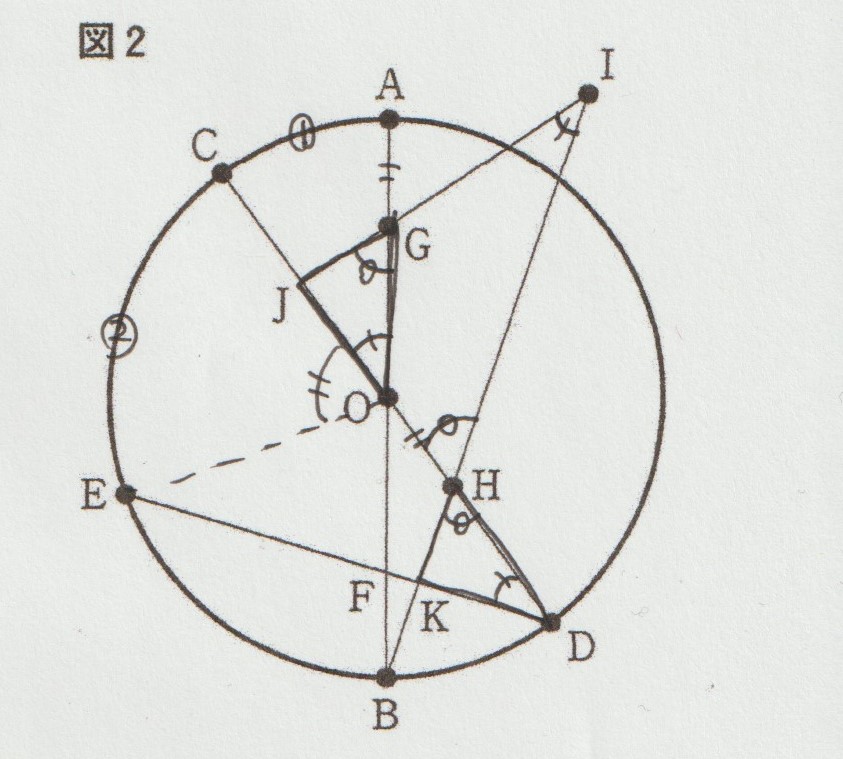
まず「弧CEの長さは弧ACの長さの2倍」であることが仮定としてあるので、弧の長さの比は角度の比と等しいことから「∠COEは∠GOJの2倍」が分かります。
一方で∠HDKは弧CEに対する円周角なので「∠COEは∠HDKの2倍」です。
このことから「∠GOJ=∠HDK」となります。
一方で「∠HIG=∠AOC」という仮定と「∠IJH=∠OJG (共通) 」という2つの条件から「△IJH∽△OJG」が分かります。
これにより「∠OGJ=∠IHJ=∠DHK」が言えますので「∠OGJ=∠DHK」も言えます。
さらに「AG=OH」という仮定もあり、円の半径をrとでも置くと「OG=DH=r-AG」も言えて、ここまで分かったことから「一辺とその両端の角がそれぞれ等しい」ので「△OGJ≡△DHK」となります。
【問2 (2) のポイント】比をそろえる
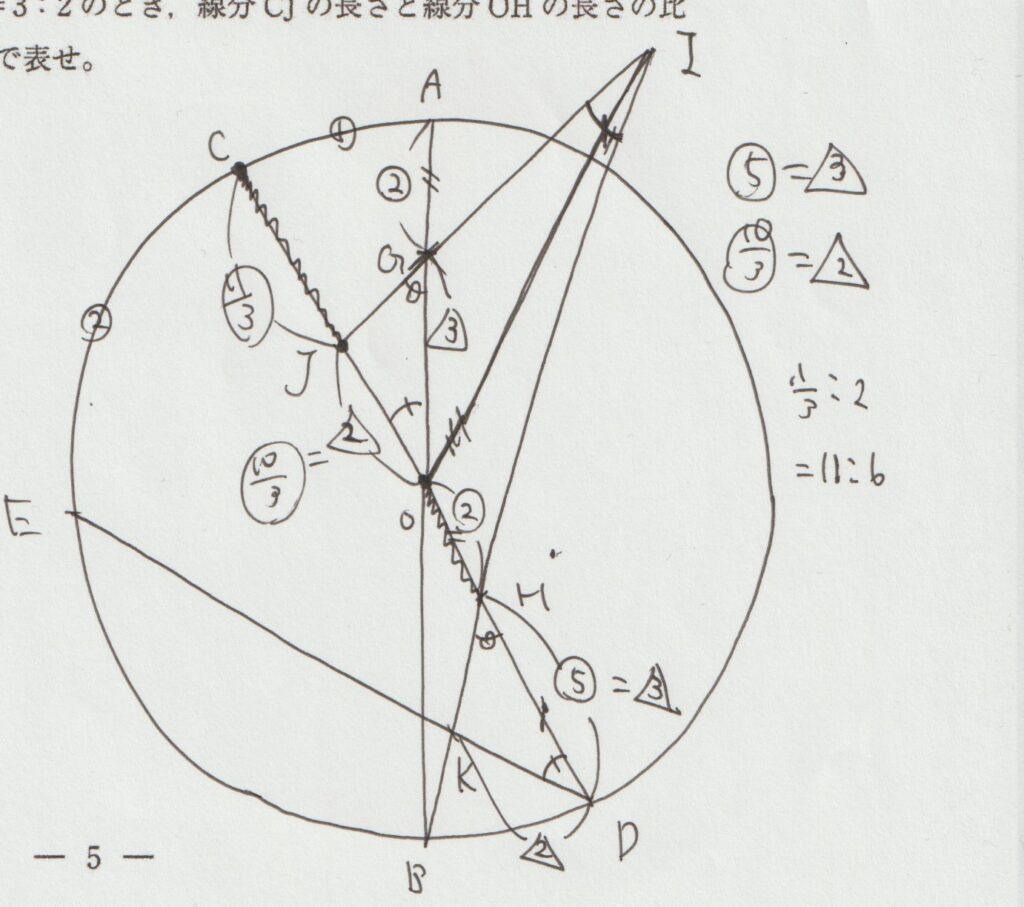
問題ではOH:DH=2:5、DH:DK=3:2とありますね。
このように、一辺を異なる2辺の長さと比べたときに「比の値が違う」のであれば「比をそろえて考えること」が大事です。
そろえ直すとOH:DH=6:15、DH:DK=15:10となります。
このように考えると、円の半径は全体で「比の値としては21」となり、 (1) の結果からOJの長さは「比の値で10」となり、CJの長さは「比の値で11」となります。
この結果から、CJ:OH=11:6となることが分かります。
まとめ
実際の解答用紙を使って記述したものがこちらです。

難関都立を受験する場合、中学3年生の夏までに「体系数学」や「新中学問題集」などのテキスト・問題集を使って「中学数学の基礎と典型的な入試問題の類題」を習得する必要があります。
特に「円周角と相似な三角形」に関する問題は「解けない問題がないようにしておくこと」が大事です。
「典型的な入試問題の類題」を正解できるようになってきたら、都立の「自校作成問題」を題材として、日比谷高校の入試対策をしていくような形となります。
私の家庭教師指導でも、こうした対策を経て「過去問で90点超え」「本番でも85点」「見事難関都立合格」を達成した生徒さんが多数いらっしゃいます。
「難関校の対策に困っている」「難しい数学の問題となるとできない」という方のために「高校受験数学対策フルサポートコース」をご用意しております。
↓高校受験対策フルサポートコース詳細↓
高校受験対策フルサポートコース – 算数・数学オンライン個別指導塾 等々力・自由が丘プロ家庭教師 (sugaku1bann.com)
「プロの個別指導で、数学を得意科目にしたい!」とういう方はぜひ一度ご相談下さい。
