こんにちは。算数・数学専門家庭教師の鈴木稔です。
私も今年で、指導歴10年を迎え、実に多くの生徒さんと関わってきたことを実感しています。
最初は中学受験の指導が、自分にできるものかと思い悩んだこともありましたが、いざ中学受験の勉強のことを調べると、なかなか面白いものだと思うようになっていきました。
指導しながら、生徒さんと一緒に学んでいくにつれて、難関中学の入試問題を私自身も解けるようになってしまったので、これからもどんどん入試問題の対策記事を書いていこうと思います。
今回は、女子学院中学の2022年度の入試問題について書いていきます。
もう既に様々なサイトで、解答が載っているかと思いますが、実際に私が解いてみた上で、「何が大事なのか」「どうすればこのような問題ができるようになるのか」について、お伝えしていきたいと思います。
この記事をお読みいただくことで、大問1で満点を取れるような、今後の対策もよく分かるようになるのではと自負しております。
大問1-(1)と(2) 四則計算
大問1-(1)(2) の計算問題がこちらです。
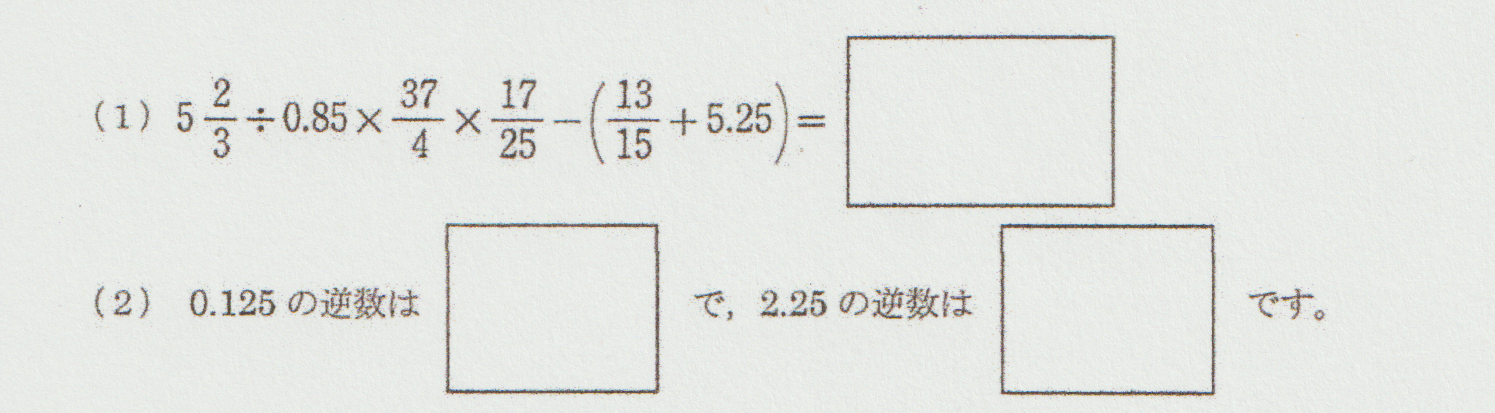
四則計算で間違えないようにするという教えを、受験生は色んな先生から受けてきたのではないでしょうか。
中学受験の算数では、「計算力」は必須です。
ではその計算力とは何かというと、この問題を見る限りは、以下のようなものであると考えられます。
・計算を進めるとき、小数のままするか、分数に直すかを判断する力
・計算の途中で約分できる力
・かけ算とわり算を含む式は「原則左から順番にする」を守れること
女子学院を受けるレベルの生徒さんであれば、このようなことは大丈夫かと思いますが、特に最後の「かけ算とわり算を含む式は左から・・・」を守れているかどうか、もう一度ご家庭でも見て下さい。
「計算は左からする」という癖が、中学以降の数学でも役に立ちます。
大問1-(3) 角度の問題
大問1-(3)の問題がこちらです。
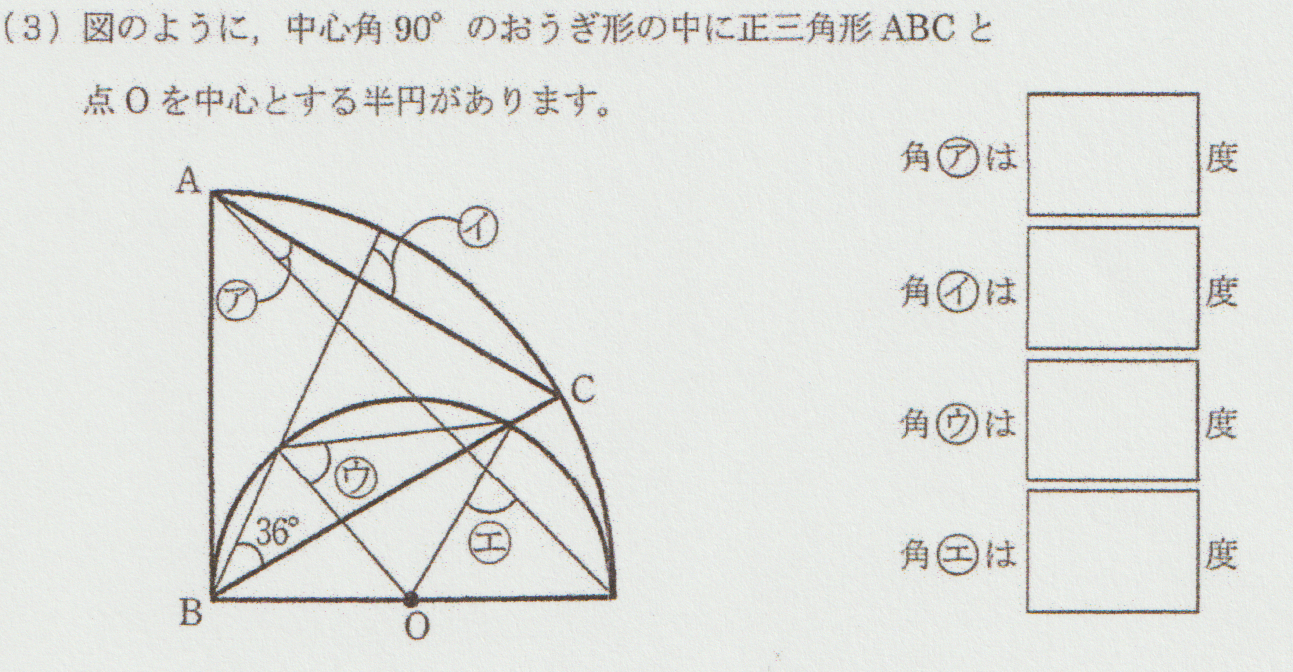
このように、「ア~エ」とありますが、必ずしも「アから順番に分かる」というわけではありません。
難関中学の入試問題を見てると、「見たことがない問題が出ると心得る」などということよりかは、「先入観を捨てる」という気持ちの方が、このような問題が出たときに役に立ちます。
図形の問題を解くとき、特に角度の問題を解く際に「先入観を捨てるために大事なこと」を、以下に書いていきますね。
角度を求めるポイント① 「明らかに分かるところ」から先に求める
この問題では「正三角形」とあるので、「60°」となるところ、「中心角90°から分かる角度」を、まずは探すことが大事です。
実はこの問題は、これをやるだけでも色んな部分の角度が明らかになります。
お子さんの様子を見て「ここが何度になるとか、決めつけてしまうことがある」と思われるときは、「明らかに、絶対にその角度になると自信を持てるところ」を探すように、お子さんにもお伝え下さい。
角度を求めるポイント② 二等辺三角形を探す
中学受験の三角形に関する問題では、「二等辺三角形を探す」という考え方をよく使います。
この問題では、なぜこの考え方が使えるかというと、「円の半径を辺にもつ三角形」があるからです。
円の半径はどこも同じ長さなので、二等辺三角形を探すのに最適な条件が揃っているのです。
「円の中に三角形があったら、二等辺三角形を探す」と思えるだけでも、十分正解できるきっかけが増えます。
大問1-(4) 円とひし形の面積
大問1-(4) がこちらです。
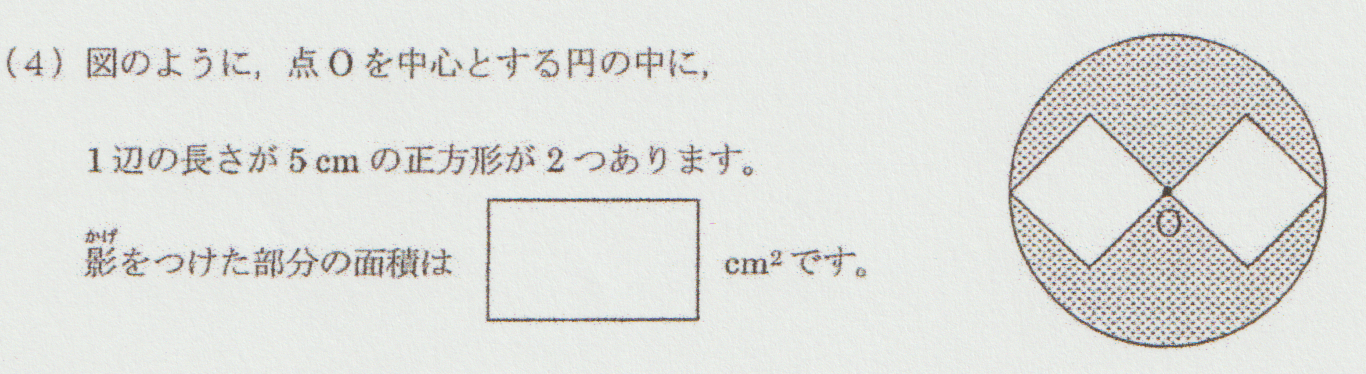
この図を見ると、「正方形の対角線が円の半径」となっています。
このようなときによく出てくる見方が「正方形をひし形と見る」というものです。
この場合、円の面積を求めないと、影をつけた部分の面積が求められないので、円の面積を求めるためにも「半径に関する情報」が必要です。
それを知るために、「正方形をひし形と見ること」が大事になってきますが、この問題では、正方形の一辺は5㎝とありますよね。
ここで大事なのが、「対角線を▢㎝とおくこと」です。
そうすることで、ひし形の面積は「対角線×対角線÷2」なので、「▢×▢÷2=5×5」という式ができます。
円の面積を求めるために「半径を2回かける」ということをしますが、上の式を見ると「▢×▢」という部分がありますよね。
これがいくつになるのかを考えられる力が、難関中の入試問題を解くために必須です。
大問1-(5) 相似な図形
大問1-(5) の問題がこちらです。

私も最初にこの問題を見たとき、「面積の比」を使うのだろうとは思っていました。
それがどこで分かったのか、以下で説明していきます。
相似な図形を見つける
問題文には「同じ印のついているところは同じ長さ」とあります。
これは言い換えると、「辺を同じ長さに分ける点がある」ということです。
このように、辺を何対何かに分ける点を「分点」と言いますが、分点が図の中に出てきたらすることは「分点同士結ばれているところを見つけ、相似な図形を見つけること」です。
相似な図形がなくても、「辺の比がそのまま面積の比になるような、二つの三角形の組」を探すこともあります。
相似な図形がなければ自分で作る!
分点同士結ばれていなければ、「自分で結び、相似な三角形を作る」ということも必要です。
「自分で結ぶ」というのは「補助線を引くこと」なのですが、「何のために補助線が必要なのか」を考えることまでセットで補助線を引くことが大事です。
大問1-(6) 速さとつるかめ算
大問1-(6) がこちらです。

大問1とはいえ、少し難しい印象もありますが、「難しい」と感じても、速さの問題は以下の手順を忘れすに解くことが大事です。
問題文をそのまま図に直す
家から駅までの距離が分かっているので、線分を描き、問題文に書いてある通りのことを、描いた図に書き込んでいくことが大事です。
図に書き込む際に、大事なことは以下のようなことです。
「どこからどこまで何分」「どこからどこまで何m」という条件を全て図に描き込む
線分を描いたら、「途中公園で遊んだところ」を、点として線分の中に書き込み、「家から公園まで何分なのか」「そのときの分速はいくらか」などの情報を書き込みます。
以下のように描けると良いのではないでしょうか。
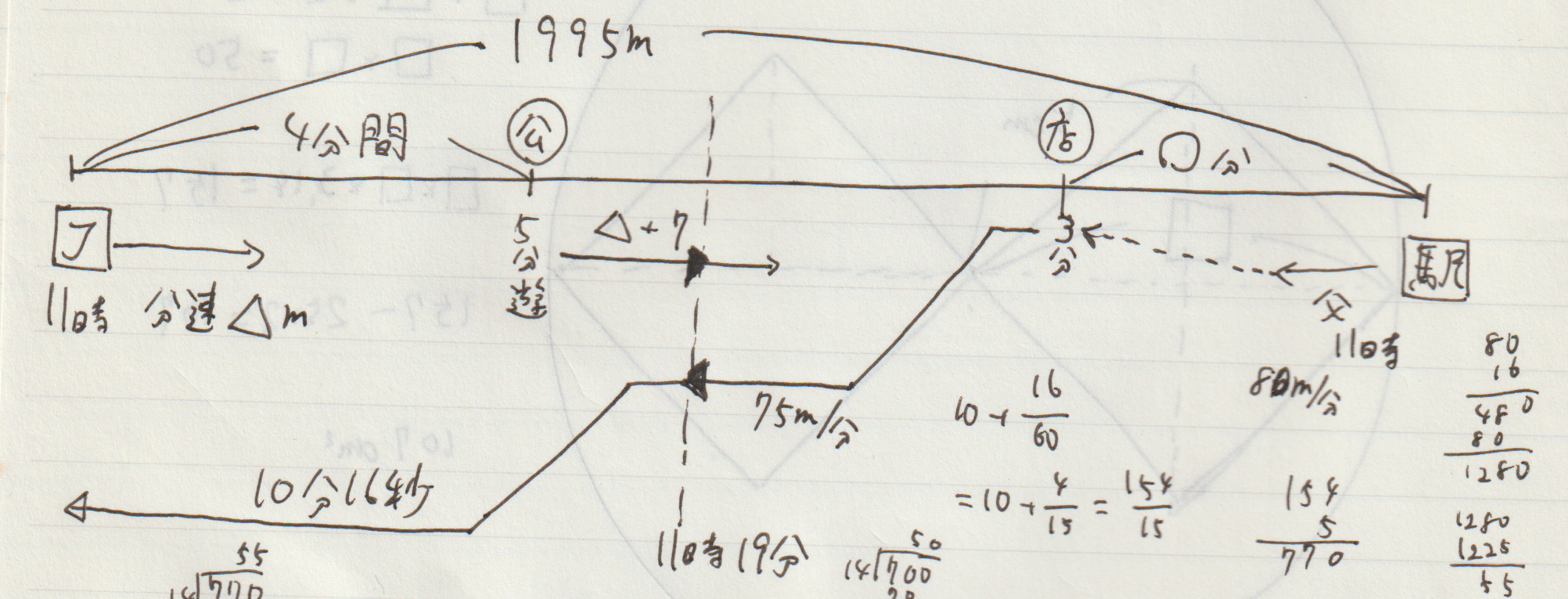
まずは「具体的な値が出るところ」を探す
速さの問題では、「分速いくらで、何分間歩いた」ということが具体的に分かる場合も多いです。
この問題ですと、「父は分速75m」「10分16秒」に注目すると、「J子さんに会ってから家に着くまでに、父が歩いた距離」が分かります。
「異なる速さで歩く」から分かること
この問題では、「父が駅からお店まで歩くのにかかった時間」と「父がお店からJ子さんと出会った地点まで歩くのにかかった時間」を足すと、16分であることが分かります。
ここで「合わせて16分」という考えが出てきます。
さらに、「父が駅からお店まで分速80ⅿ」「お店から出会った地点まで分速75ⅿ」とあるので、父が移動した距離は、このような面積図で表すことができます。
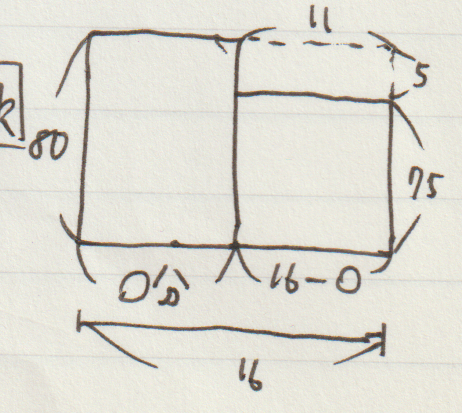
面積図で解ける問題を「つるかめ算」と言いますが、大事なのは「なぜ面積図が使えるのか」「その理由はどこで分かるのか」が理解できることです。
面積図を使う問題であることは、以下のような条件二つを問題文で見つけることで、納得できるようになります。
・かけ算で求める量があること (この問題の場合は速さ)
・「合わせていくつ」が明確な量があること (この問題の場合は父が歩いた時間)
この二つに注目できることで、「面積図を使うこと」が思いつくようになれます。
大問1で満点を取るための勉強法
これまで、具体的な問題についての解説をしてきました。
女子学院中学ともなると、「大問1では満点を取ること」が基本的です。
おそらく全ての中受の算数に言えると思います。
そこで、この記事では最後に、「女子学院レベルの算数の入試問題」において、大問1で満点を取れるようになるために大事なことをお伝えします。
四則計算は「できない問題がない状態」を作る
難関中学を受けるのであれば、四則計算や逆算に関しては「ここまでできれば大丈夫」という問題はありません。
四則計算だけでも、他の難関中学の過去問などにも手をつけて、「必ず正解できる」「できないことがない」という状態にしておくことが大事です。
そのためにも、特に難関中学を目指す小4、小5のお子さんは、四則計算は毎日やる時間を確保して下さい。
図形は実際に描く
図形の問題は、中学受験の場合は「問題文とともに、あらかじめ描かれた図形」が与えられていることの方が多いです。
しかし、どうしても与えられた図形の中に数値を書き入れてみたりすると、「どこの長さがいくつなのか」「どこの角度が何度なのか」が分かりにくくなってしまうことがあります。
特に難関中学を目指すのであれば、図形の中に書き込むことも増えますよね。
このような理由から「与えられた図形と同じ図形を、もっと大きくノートに描くこと」が大事です。
具体的には、ノート1ページ分全て図形を描くことに使うようなイメージです。
図は「綺麗に描く」よりかは「大きく描く」を意識しておくことが大事です。
よくある問題を全てできるようにする
よくある問題というのは、例えば「予習シリーズ」でいうところの「練習問題のページにある問題とその類題」だと思って差し支えありません。
サピックスにお通いの方であれば、算数の先生から「必ず宿題で出ている問題とその類題」が、まさに「よくある問題」です。
そのような問題を教わった後に、同じ考え方で解ける問題を「ヒントや解説など何も見ずに正解できるようにしておくこと」が大事です。
まとめ
以下、実際に私が解く際に使った用紙を載せます。
動画でも解説する予定なので、そちらもご覧いただき、この記事も参考に、問題演習していただければと思います。

[…] […]