こんにちは。算数・数学専門プロ家庭教師の鈴木です。
この記事では、見直しをするということに関して、具体的に何をすることなのかを解説していきます。
一言に「見直しをする」と言っても、問題を解くプロセスにおいて、「いつ」「どこで」「何するのか」を明確にしていくことが大事です。
以下の記事では、見直しをかける上で重要な「いつ」「どこで」を明確にまとめた「見直しのタイミング」について書いています。
https://sugaku1bann.com/2021/11/10/minaosinotaiminngu/
当ブログでは先に「見直しをするタイミングがどこにあるのか」を述べてから、そのタイミングで何をするのかを書くことにしました。
というのも、さまざまなお子さんを見てきて、見直しすることを分かってはいても「問題を解くプロセスにおけるどの場面で見直しをすれば良いのか?」が分からないお子さんもいたためです。
ここからは、上の記事で解説してきた「見直しのタイミング」において、ミスをなくすために、具体的に「どう行動すれば良いのか」について述べます。
その前に、まずは一番重要なことをお伝えしていきます。
ミスの原因が何かを知る
ミスをなくすための第一歩は、自分がどのタイミングで、どんなミスをしていたのかを知ることです。
それができることで、見直しのタイミングにおいて、自分が何をすればミスが防げるのかが分かります。
例えば問題文を読んで、文章を図に描き起こすまでは合っていたのに、図から計算式を立てるときに、違った計算式を立ててしまったとします。
このときに、それが「図を見間違ったことによるもの」なのか、「式を書き間違ったものなのか」で、ミスを防ぐ対策は変わってきます。
もし「図を見間違った」のであれば、図中に必要な数値や情報が、余すことなく書いてあったかどうかを振り返り、「図中に何が書いてあったのか」を目で見て確かめながら式を立てることが「ミスを防ぐ対策」になります。
そして、図と計算式を見て、計算式が図を再現しているかどうかを確かめることが「見直し」ということになります。
以下ではこうした考え方のモデルを基本として、「ミスを防ぐ方法」や「見直しの仕方」について述べます。
問題文を振り返る際に確かめること
問題文を読んで、どんな条件があったのかを把握するときには、問題文の読み方が正しかったどうかを確かめる必要がありあります。
つまり、「自分勝手な解釈をしていないかどうかを振り返る」ことが大切です。
問題文の読み方が正しいかどうかを確かめる際に重要なのは「過去にこんな文の読み方をして良かったのか?」を思い出すことや、問題文の読み落としがないかを確かめることです。
ここではどうしても、問題演習量が多いかそうでないかで、問題文の読み方が正しいかそうでないかを判断できる力が変わってきます。
算数・数学では特に「~について」であるとか、「~となる点P」という書き方に代表されるように、一回問題文を読んだだけでは「それが何のことを言っているのか」が明らかにならない場合があります。
そうした状況下においても、「過去に似た文章が出てきたときに、どの言葉がどの量のことを指していたのか」、問題文として書いてあることを「どう言い換えるのか」を思い出すことができると、問題文が理解できてきます。
「この量は、文中にあるこのことを言っているんだな」といった判断の仕方ができると、問題文を読む際の確かめ方の精度も上がります。
もし、そうした判断の仕方ができていないというのであれば、まずは基本問題を学び「問題文の読み方」を身に付けていくことが大事です。
一方で、文章の読み方は正しいのに、問題文にある条件を「見落としていたこと」が原因でミスをしていた場合は、日頃から問題文を音読するなどして、「黙読だけに頼らない勉強法」に目を向けることも大切です。
ミスをなくすための図の描き方
ここからは、図を描く際にどのように描けば良いのか、描いた図が正しいかどうかを知るにはどうすれば良いのかについて、お話していきます。
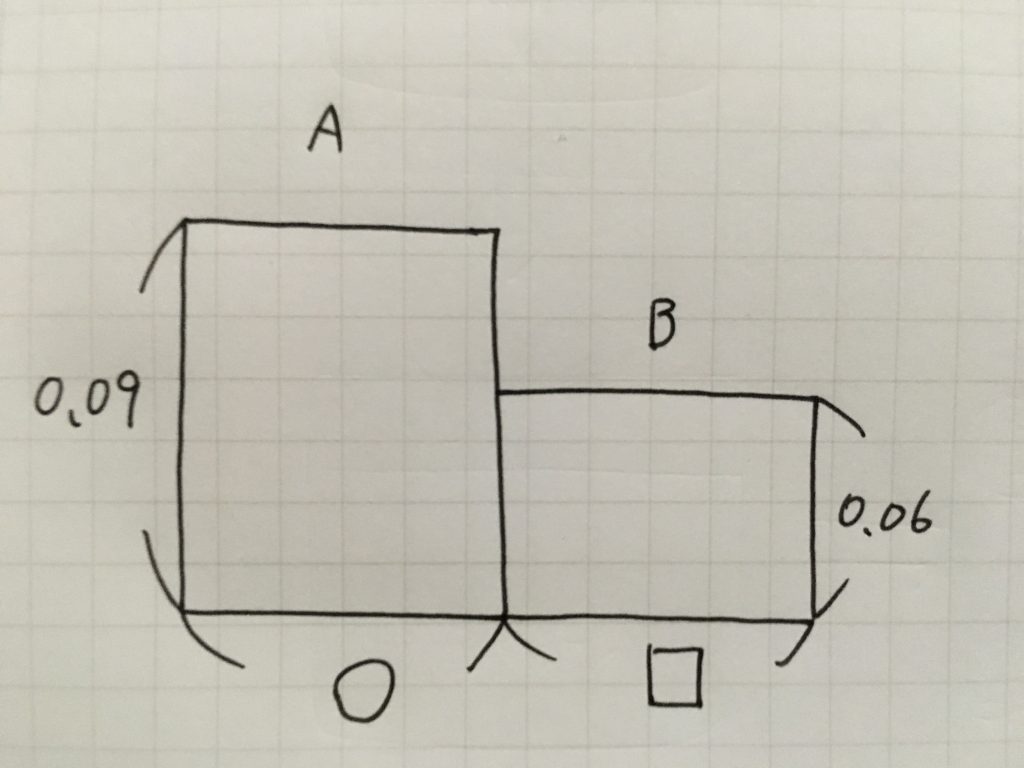
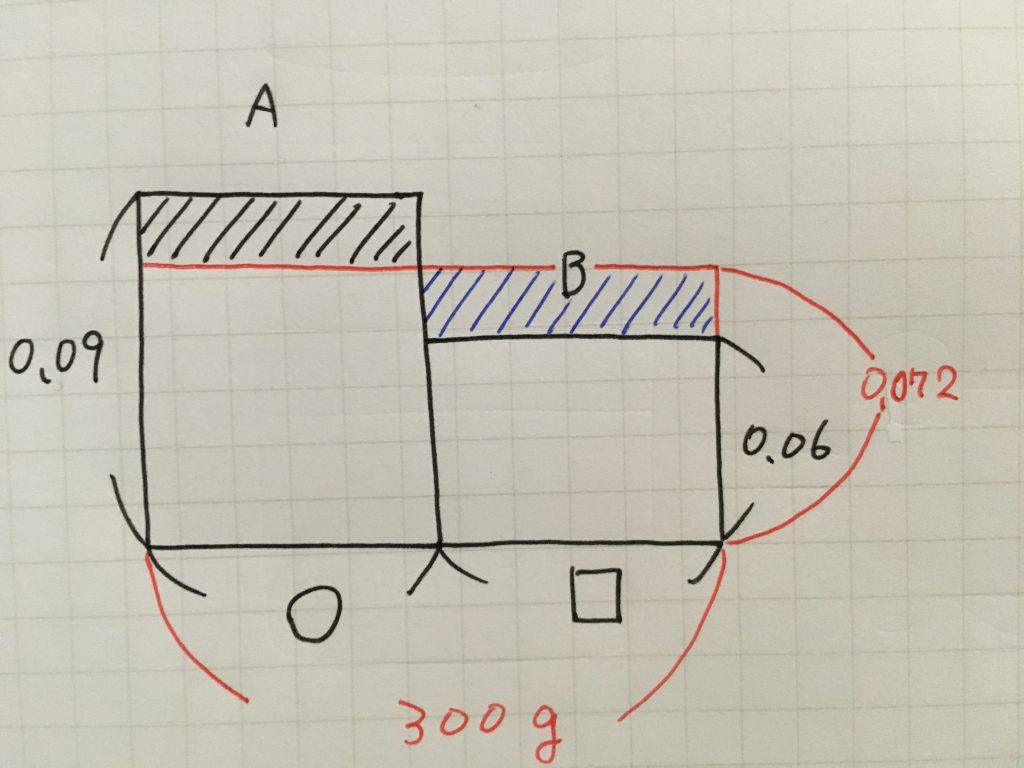
図は大きく描く
まず大切なことは、図は大きく描くということです。
ノート1ページ分全てに図形やグラフを描くなどして、「どこからどこの長さがいくつなのか」「どこからどこの角度を文字として置いているのか」といったことが、すぐに分かるようにしておくことが大切です。
。
図をそれくらい大きく描くことを意識した上で、自分が描いた図が正しいものかどうかの確かめ方について、以下で述べていきます。
描いた図の正しさを確かめる方法
問題文を読み、それを図に描き起こしたときに、その図が合っているかどうかが分からない限り、式を立てたりすることは難しいはずです。
ここでいう図とは、中学受験の算数であれば、線分図や面積図といった「文章を視覚化したもの」、三角形などの図形、グラフを意味するものとします。
「描いた図が合っているかどうか」については、問題文と描いた図との間を行ったり来たりしながら、そのことを確かめる必要があります。
ですので、答え合わせをして、答に載っている図が自分が描いた図と違っていた場合、「問題文を読み間違えていること」や「図の位置関係などが違っていること」、「図の中に書き込んだ情報が違うこと」などが考えられます。
問題文を読み間違えているのであれば、問題文の振り返り方に課題があるので、前の節でも述べたように、「正しい問題文の読み方を学ぶこと」や一回でも音読をすることが大切です。
「図の位置関係や書き込んだ情報」などが違っているのであれば、例えば図中に「点Aや点B」などといった記号を書き入れる際に、「本来Aと書くところをBとしている」などのミスがないかどうかを確かめることが大事です。
このことは、三角形などの図形を描くときに、「角度や長さがいくつなのか」といった条件を書き間違っていたり、「間違っているのに正しいと思い込んでいること」を書いていないかどうかを確かめることとも関連があります。
一つ例を挙げると「AくんはBさんの2倍の金額を持っている」という文章があったときに、線分図を描き「BさんがAくんの2倍の金額を持っていること」を表す図になってないかどうかなどを確かめることが見直しです。
上に書いたようなミスが、問題文に書いてある記号などを見間違ったこと (読み間違ったこと) が原因で起きたのであれば、問題文をもう一度振り返り、数値や言葉に線を引くことなどがミスを防ぐ対策になります。
「書き間違い」が原因で起きたのであれば、自分が書いた図が正しいかどうかを、問題文と共に振り返ることが、ミスを防ぐ対策になります。
つまり、自分が描いた図の位置関係や、図中の記号・数値を見て、それらが問題文において説明されているものと一致しているかどうかを、目で見て確かめながら、書き間違いがないかをチェックしていくことが見直しです。
まとめると、問題文の読み方は正しかったのに、描いた図が違っているということがある方お子さんは、「図に書き入れた記号や値と、それらをとりまく位置関係」が正しいかどうかを確かめる必要があります。
そのときに、もちろん問題文を振り返ることも大事ですが、「自分が描いたことを何度も見て、問題文を再現したものになっているかどうかを確かめる」といった振り返り方に重きを置けると、図の見直し方が身についてきます。
そもそも図に「記号や値」を書き入れていないのであれば、それらを書くクセをつけることが大切です。
「問題文にある情報はすべて図の中に反映させる」ということが、基本スタンスとしてはあります。
自分が立てた式が正しいかどうかを振り返る
問題文を読んで、読み方も合っていて、描いた図の位置関係なども正しいのに、計算式が間違っているということも、ミスの原因になってしまいます。
問題文と描いた図の間を行ったり来たりしながら、図の正しさを確かめるのと同様、今度は「描いた図、あるいは問題文と自分が書いた計算式との間」を行ったり来たりしながら、式の正しさを確かめることになります。
その際に意識することは、以下の3点です。
・その式は何を求めるためのものか?
・その式は何と何が等しいことを表すのか?
・どの量とどの量を何算するのか?
まず一つ目は、「その式は何を求めるためのものか?」を気にすることです。
その式は何を求めるもの?
例えば速さの問題で、「速さを🔲とおいて、距離が等しいことを意味する式を作る」という場面があります。
例題を考えると、5分歩いた結果150m進んだことが問題文から分かった場合、速さを🔲として式を作るときに、「分速xmで5分歩いた結果、150m進んだこと」を意味する式は「🔲×5=150」となります。
この式は、「速さを求めるために作る」ということを目的として作ります。
しかし、お子さんの様子を見て、「150÷5=30」といった具合に、いきなりかけ算や割り算をしてしまう場合、そもそも「何を求めるのかを意識して問題を解く」という視点があるかどうかを見る必要があります。
速さの問題を解く際に式を作るときは、「そもそも速さとは何のことか」「公式 (正しくは定義という場合もあります) はどういう形をしていたか」を思い出しながら、書いた式が正しいかどうかを確かめていきます。
一般的に「何を求めるのか?」を意識して式を作るときには、式の中に出てくる値や文字が、言葉として何を表すのかを振り返ることが大切です。
そして、上に書いたように、「公式がどういう形をしていたか?」を思い出すことが、意識するポイント二つ目の「何と何が等しいのか」を確かめることにつながります。
何と何が等しいことを表すのか?
例を挙げると、速さの公式は「速さ=距離÷時間」(速さは距離を時間で割ったものに等しい) 、食塩水の濃さの公式は「濃さ=食塩の重さ÷食塩水の重さ×100」(濃さは食塩の重さを食塩水の重さで割ったものの100倍) となっていますよね。
これらの公式はどれも「この量は何かと何かをかけ算 (割り算) したものと等しい」ということが、分かる形で書いてあります。(少し細かい話をすると、「この量はこうして出すものとして決めます」ということです)
公式をこのように、形として覚えることはもちろん大切です。
その際に、覚え方として「どれとどれを何算したものが、結果としてどういった量を表すのか」まで意識することができると、それがそのまま「立てた式が合っているかどうか」を確かめるための意識にもつながります。
どの量とどの量を何算するのか?
意識するポイント三つ目は、「どの量とどの量を何算するのか」ということですが、このポイントは、「カッコを使う式」を立てる際に役に立ちます。
具体例でいうと、「1000円出して、50円の消しゴムx個と80円のえんぴつy個買ったときのおつり」を、xとyを使って式として表現するときなどです。
正しい式は「1000−(50×x+80×y)」となりますが、この式は「持っているお金から、消しゴムとえんぴつの合計金額を引き算する」ということを表します。
本当はこうした式を書くのが正解なのですが、本当によくあったのが「1000−50×x+80×y」としてしまう書き間違いです。
上の式が表す意味を、お子さんに聞いてみたこともありましたが、考えていることは合っていたものの、書いた式としては、「おつりとなる金額を意味していない」という理由で、合っていないものになってしまいます。
こうした式を書いてしまわないためにも、「何と何を足せば良いのか」「何から何を引けば良いのか」といった考えを持つことが、書いた式が合っているかどうかを確かめることにつながります。
以上三つのポイントを意識した上で、「書き間違い」「見間違い」がないかどうかを確かめることが、式を立てるプロセスにおける見直しということになります。
「上の式」=「下の式」かどうかを確かめる
計算式を立てることができたら、あとは答を出すために、その式を計算する場面があります。
先ほど、「式変形をするタイミングで見直しをする」というお話をしましたが、ここからはその続きとしての意味も込めて、式の正しさの確かめ方について述べていきます。
計算式は、まず左から右へとイコールでつないで、そのあと上から下へと式をつなぐことになりますが、こういった書き方は教わるだけでなく、実際に書く場面がないと、なかなか身につかないものです。
小学生の場合だと、筆算することの方が多い場合もありますが、四則が混ざった式を計算するときには、どうしても式を上から下へと書かないと、計算のスペースもなくなってしまいます。
そのときに大事なのが、上の式と下の式をイコールで結ぶときに、「上の式は本当に下の式と同じかどうか」を確かめることです。
例えば 100−30÷0.75 という式があったとします。
この式の計算の仕方はさまざまありますが、まず
100−30÷0.75=100−30÷(3/4)
といった具合に、小数を分数に直したとします。
このとき、左の式と右の式が合っているかどうかを、「符号を書き間違えていないか」「数を書き間違えていないか」「小数と分数は本当に同じか」を見ながら確かめていきます。
特に小数を分数に直すときに、例えば「0.25=1/5」としてしまうなど、書き間違いなどではなく、「本当にそうなると思った」などの「思い込みがないか」を気にしておくことも大切です。
この例だと、「0.75」が「3/4」になるのは問題ありません。
しかし、分数を小数に直すときに、「分数でいうどの数がどの小数に対応していたか」を覚えているお子さんであっても、計算を進める際に、覚えていることが合っているかどうかを考える場面を作ると良いです。
そうした確かめを経て、「100−30÷(3/4)」の下に、計算式を続けて書いていくわけですが、今度は30÷(3/4)を計算する場面があります。
「÷」を「×」に直した式を書いていくのが、最も「何をしているのかがよく分かる式」ですが、「100−30÷(3/4)」という式から一度離れて、「30÷(3/4)」を直接計算しても問題はありません。
ただそのときに、やはり「30÷(3/4)」が合っているかどうかを確かめることや「100−30÷(3/4)=100−40」と上から下へと式をつなぐときに、「数を書き間違えていないか」などを確かめることが大切です。
この例から分かることは、上の式と下の式が同じかどうかを確かめるときに大事なのは、以下のポイントを意識することです。
・「上と下で書いてあることの中に、お互いに違いったところがないかを見る」
・「式の途中で優先的に計算するところがあれば、その答が正しいかどうかを気にする」
なお、中学以降の数学では、計算式を上から下に向けて書くことがもっと増えます。
a−(−b+c)+(−2a+3b−5c)=a+b−c−2a+3b−5c
=−a+4b−6c
といった具合に、上の式と下の式を「イコール」で結ぶことが増えます。
このとき、「上に書いた式と下に書いた式が同じかどうか」を確かめるために、見間違いがないかであるとか、書き間違いがないかどうかを気にすることが大切です。
中学以降の計算では、例えば「5-3」を「5+(−3)」と捉えた上で式を計算することなどを例に、「演算の捉え方が正しいかどうか」を確かめることも出てきます。
この例を代表的な例として、中学の数学からは「式はすべて足し算の記号で結ばれる」という見方を受け入れることが、計算結果が正しいかどうかを判断するための道具の一つになります。
それができた上で、いわゆる符号の書き間違いであるとか見落としがないかを確かめることが、上の式と下の式が合っているかどうかの見直しということになります。
「どういう意味で同じなのか」を理解する
タイトルにもあるように、どういう意味で「同じ」なのかを確かめる場面が、中学以降の数学で出てきます。
これはいわゆる「同値性」というもので、お互いに一見別の形をしているものがあったとしても、それらが満たす条件が同じであれば、両者は同じとみなすという考え方です。
算数で出てくることはほとんどないのですが、中学では「方程式」の単元ではじめて出てきます。
簡単に、(2x/5)=10 という方程式を例に、「どういう意味で同じなのか」を確かめる場面がどこにあるのかについて、お話していきます。
そもそも「方程式を解く」とは、「左の式と右の式をイコールでつなぐのであれば、xに入る数はいくつなのかを答えること」という意味を持ちます。
上の式を見ると、左の式は分数の式となっているので、これだとxに入る数を求めるにも、よく分からないということで、両辺にまずは5をかけるという場面があります。
そうすると式は 2x=50 となり、xの値を求めることに近づきます。(x=25)
さて、はじめにあった (2x/5)=10 と、2x=50 は、方程式の形は違っても、これら2つの式にx=25をあてはめてみたときに、どちらの式においてもイコールの関係が成り立つという意味で、2つの方程式は同じとみなせます。
よくある間違いが、以下のようなものです。
(2x/5)=10=2x=50
この式では、全ての式を「イコール」で結んでしまっていますよね。
こうした式を書いてしまう原因として、「方程式を解くとはどういうことか」「イコールの記号の意味」「どういう意味で同じか」を意識しながら、式の計算をできていないことが考えられます。
ここでは、左の式と右の式に5をかける場面が出てきましたが、この例をモデルとして、「はじめにあった左 (または右) の式に、何か数をかけた式を計算していく過程でミスがないかどうか」を確かめることが大切です。
このときもやはり、「書き間違い」、「書き忘れ」、「見間違い」、「見落とし」を防ぐために、もとの式がどんな式になっていたのか、自分が書いた式に問題はないかを見ていくことが見直しの一つです。
そうしたミスがないかどうかの確かめを経て、イコールなどの記号でつながれた式を式変形していくときや、そもそも左の式と右の式を「イコール」で結ぶときに、「何をもって同じなのか」を振り返る場面が、数学を学んでいく上ではよく出てきます。
その振り返りこそが、自分が行っている計算プロセスが正しいかどうかを確かめるための、見直しの一つでもあります。
暗算は自分の許す範囲を決める
これまで見直しの仕方に関して、「どのタイミングで」「どんなことをするのか」について述べてきました。
ここからは、まずは暗算に関することについて、お話をしていきます。
これまでは、問題文を読み、それを図に描き起こすタイミングで見直しをすることや、図を式に直すとき、式を変形していく過程において、見直しのポイントがあることをお伝えしてきました。
しかし、実は式変形していく際に、暗算に頼っている部分も多くあるのです。
例えば、先に出てきた「2x=50」という方程式を、小学3年生が解こうとしたとします。
「方程式」という考え方を知らなくとも、「2に何をかけて50になる?」と聞いたときに、割り算で「50÷2」を計算してあげれば良いことが分かれば、「50÷2」を筆算にてすることで、答を出せることもあるかとは思います。
しかし、既に「方程式」とは何かを知っていて、与えられた数が「どの数とどの数のかけ算でできているのか」といったことも分かるような人が、わざわざ筆算をする必要はないのです。
それこそ、「暗算」で答を出しても問題はありません。
このことは、何を意味するかというと、タイトルにもある通り、「暗算が許される思考の範囲」というのは、人それぞれ違うということです。
ですのでもし、何か式を計算したあとに、具体的に「数同士の計算」においてミスがあったと分かったときには、そのときに自分は「暗算」だけで計算をしていなかったかどうかを確かめる場面が出てきます。
その場面において、本当に暗算が原因で答が間違っていたことが分かったのであれば、自分で筆算の式を書くことや、数を具体的に書いておくことなどが、暗算によるミスを防ぐきっかけとなります。
綺麗な字を書けるようにするための対策
親御さんから、「子どもの書く字が汚いのですが、どうしたら良いですか」というご相談を受けることが多くあります。
そうしたご相談に対して、解決策の一つをここで提示する前に、先に大切なことを言うと、どんな字を汚いと思うのかは、個人の主観によるところが大きいということです。
親御さんから見ると、お子さんの書いた文字や数字、図などが汚いなと感じたとしても、お子さん本人からすると、「汚い字や図」を書いたつもりはないということも、しばしばあります。
ただ、明らかに字が汚い(そう見える)ことで、問題を解くプロセスにおいて、「見間違い」や「書き間違い」によるミスが横行しているのであれば、まずはお子さん本人に、その事実に気づいてもらう必要があります。
どうすれば、そうしたことに気づいてもらえるのかについては、またあとで述べることにして、概ね「汚い字」とはどんな字なのかを、それこそ「私の主観」ではありますが、お話していきます。
字の大きさを揃える・字と字の間を離す
「汚い字」というよりかはむしろ、「大きさが揃っていない字」「字と字の間に空きがない文や式」を書いてしまっていたお子さんは、「見間違い」や「書き間違い」によるミスをする確率が、かなり高いと言えます。
このタイプのお子さんの書く字を見てみると、大きさが揃っていないだけでなく、数や文字式において「どの文字をどこの位置に書くと見やすいのか」といったことを、意識できていない書き方になってしまっていることも多いです。
第三者から見て、こうした字でもってノートを取っているお子さんは、「ノートをもう一回見返すことがあるかどうか」を聞いてみると、高い確率で「見返すことはない」という答が返ってきます。
算数・数学を学んでいく上で、「振り返ることや見返すこと」は必須となってくるので、自分が書いたノートを振り返ることなどは、習慣として身につけていく必要があります。
そうした習慣を、当たり前に身に付けられるように、まずはできることとして、「書く字の大きさを揃える」というところから、直していくことが大切です。
さて、この節の最後に、お子さんがどうすれば「汚い字」によってミスをしたことに気づいてもらえるのかについて、実際にあったことを例に、お話していきます。
答を出したプロセスを振り返る
お子さんが出した答が違っていた場合、まずはお子さんがどうやって問題を解いたのか、そのプロセスを振り返ってみることが大切です。
綺麗ではない字で書いてしまっていても、問題を解くための考え方は合っていることはよくあるので、合っていることに対しては、承認をかけていくことで、お子さんの中にも安心感が生まれます。
解き方を説明してもらう
答を出すプロセスを振り返ると同時に、お子さんに、自分が書いたことに沿って、「どんな式を立てたのか」「なぜその式を立てたのか」といったことなどについて、説明をしてもらう場面が必要です。
汚い字のせいでミスをした可能性が高い場合、そのことに気づいてもらえるように、「自分が書いた文字や数字」を読み返しながら説明してもらうと、必ずといって良いほど、お子さん自身がミスを見つけることができます。
これまでも「問題文」や「自分が考えたこと」などを振り返ることの重要性をお伝えしました。
ですので、親御さんから見て明らかに「字のせいでミスしているのでは」と考えられる場合、お子さん自身が自分で書いた字を、もう一度見るということが大切です。
どんな字を書けば良いのかを考える
お子さんが自分の書いた字を振り返る場面を作り、その場面において「書き間違い」や「見間違い」が原因でミスをしていたことに、気づいてもらうことが必要です。
そのためには、まずはお子さん本人に、「字を書くプロセスにおいて何が起きていたのか」を聴くことがポイントになります。
そのことについて聴いた上で、お子さんが以下に書くような質問に答えることができると、「汚い字」によるミスを防ぐことにつながります。
①「本来何を書くべきところを、間違ってどんなことを書いていたのか」
②「自分が書いた字をどう認識していたのか」
③「どんな字を書けば、ミスを防げるのか」
特に②と③の質問は、「自分がこんな字を書いていた結果、こんなミスをしたから、これからはもっとこういった字を書けば良い」という解決策を見い出すことにつながります。
実際に、私の指導でも、こうした会話のプロセスを経て、生徒さん本人が「綺麗な字」を書いてくれたという場面もありました。
本人が「こんな字を書くのは良くない!」ということに気づき、それを自ら直すまで待つことが大切だと感じます。
自分が出した答=求めなさいといわれているもの?
計算した結果が合っていても、問題文で「これを求めなさい」と言われているものが出せているかどうかを確かめることが大切です。
そのためには、自分が出した計算結果などに対して常に、「今自分は何を求めたのか」を振り返ることが大切です。
返ってきたテストを見て、例えば答を書いているのに✖がついている部分が目立つとします。
そのようなとき、「お子さんが答として出した(つもりになっている)もの」と「問題文で求めなさいと指示されているもの」との間に相違がないかどうかを見て下さい。
もし、ここで書くように、「問題文において指示されているものではないこと」を答として書いている場合は、普段からノートの書き方を整えていくことが、ミスを防ぐ対策になります。
具体的には、ノートには計算式だけではなく、計算した結果に対して「これはどこの何の値」というように、求めた値や描いた図に対し、「問題文でいうところの何のことを指しているのか」が分かる情報を載せておくことです。
こうした描き方ができるためには、話が戻りますが、やはり図は大きく、ノート一面に描くくらいの意識を持っておくことが大切です。
特に図を描く問題で、例えば点が動く問題などではどうしても「点が動く結果どんな図形ができあがるのか」「その図形ができるのはいつのことなのか」を把握しておく場面があります。
そういったことを把握しつつ、もう一度問題文を振り返り、「自分が出した計算結果」や「求めなさいと指示されていること」が一致していることを確かめた上で、解答用紙に答を書くというプロセスを身につけることが大事です。
まとめ
見直しと言っても、各問題を解くプロセスにおけるどのタイミングで、何をすることなのかを、具体的にお子さんに伝えていくことが大事です。
お子さんにとっては正解を出せたはずなのに、答が間違っていた場合、「間違った知識・考え方を正しいと思い込んでいること」であるとか「見直しの仕方を知らないこと」が、その大きな原因として考えられます。
お子さんが間違った知識などを「どんな風に正しいと思い込んでいるのか」については、以下の記事でも解説してありますので、気になる方はぜひご一読下さい。
https://sugaku1bann.com/2021/10/31/misudewanakutisikibusokukanntigai/
ここでお話してきたように、各見直しのタイミングにおいて、「見間違い」「書き間違い」がないかどうかを確かめていくことはもちろん、「考えていることが正しいかどうか」を振り返ることも、立派な見直しです。
見直しとは、ただ自分の解答を流し見ることではなく、その都度「合っているかどうか」を振り返ること、目で見て確かめることです。
この記事を、どうぞ見直しのお役に立て下さいね。








[…] […]
[…] http://sugaku1bann.com/2021/11/20/minaosinosikata/ […]
[…] https://sugaku1bann.com/2021/11/20/minaosinosikata/ […]