都立国立高校の入試数学　　問題の考え方とその対策

こんにちは。世田谷区の数学専門コンサルタント鈴木です。

今日は、都立の最難関、国立高校の入試問題を見ていきたいと思います。

難関高校の入試を受ける方からは

とにかく、数学さえ何とかなれば！

という声をよく聞きます。

今のうちから、このくらいのレベルのことを、どの程度練習しておくべきなのかを知ってほしいという思いから、この記事を書くことにします。

計算問題は、高校の数学を意識した計算力を身に付ける

問１．√は、必ず有理化すべし！

√が入った計算式は、とにかくまずは有理化しましょう。

その方が、後で計算が楽になります。

問１では、√がかかった数は、文字として捉えるという考え方が基本です。

()の２乗の計算は、展開公式に沿って計算することも、意識しておいて下さい。

問２．文字式・方程式の違いを押さえる

問２は連立方程式ですね。

ここでは総合的な計算力が求められます。

文字式の扱い方、「方程式を解く」とは何をすることなのか

を常に意識して、今自分は何の計算をしているのかを、しっかり把握していきながら計算していくことが大事です。

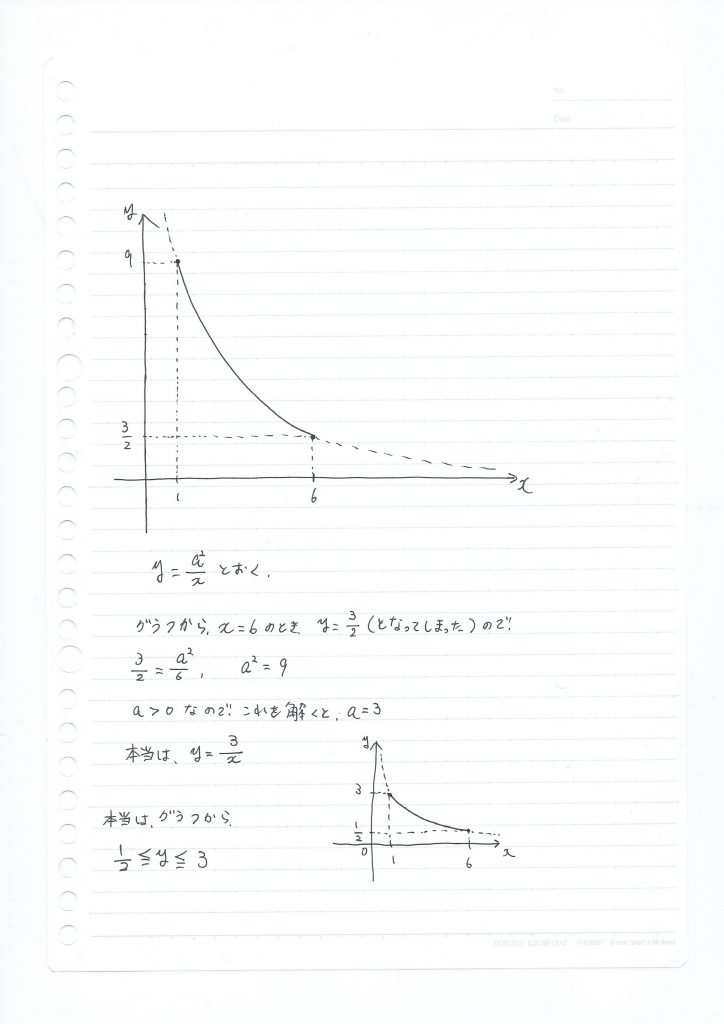
問３．関数は計算だけではなくグラフも描く

問３は、反比例、関数についての問題です。

それも、変域についての問題です。

反比例に限らず、関数全般において、グラフを描いて考えることは必須です。

このことは、高校の数学になると、ますます重要になってきます。

関数の問題を考えるときは、いつも頭のかたすみに

「ｘがこの値のときに、ｙはいくつになるのかな？」

という意識があると、必ず、得意になっていくはずです。

問４．確率　選び方・並べ方を求める式を理解する

この問題は、選び方と並べ方の違いに理解があるかどうかで、差がつくのではないでしょうか。

特に、この問題文にはAの袋に残っている２枚のカードとありますね。

Aの袋から取り出した２枚のカードを使って、数字の和を考える訳ではないのですが、ここで

Aの袋のなかにある４枚から２枚取り出して数字の和を作る場合と、Aの袋に残っている２枚のカードから、数字の和を作る場合とでは、やっていることは違っても、その場合の数は同じ

ということに、気づくことが求められます。

日頃から問題文を読んで、「選ぶ」のか「並べる」のかを、正確に考える力が大事です。

問５．作図はとにかく、二等分線を描くことに帰着せよ

２２．５度と書いてあるのを見て、すぐに４５度の半分だと、気が付いたもの勝ちな気がします。

ただ、その４５度をどう作るのかが問題ですね。

そのために、まずは線分BCの垂直二等分線ｌを作ります。

すると、半円Oと直線ｌとの交点をRとすれば、∠ROB＝４５度となります。

ここで、今度は円周角の定理から、あるところがもう、２２．５度になっているのですが・・・

お分かりですか？

∠RAB＝２２．５度となります。

弧BRの円周角は∠RAB、弧BRの中心角は∠ROBなので、お互いに２倍、１/２倍の関係です。

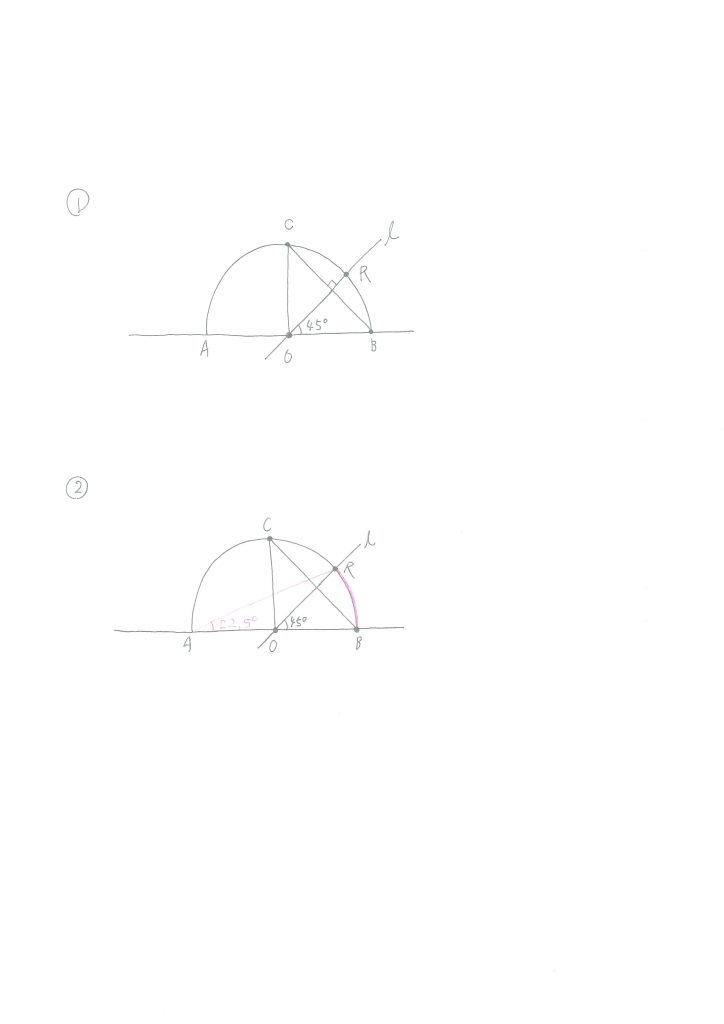
すると後は、線分ARに平行で、なおかつ半円Oと接する直線mが描ければ、半円Oと直線ｍとの交点が、まさに求めるべき点Pとなります。

が、しかし、別に直線ｍを求めなくても良いのです。

むしろ、まず求めるべきは、線分ARの垂直二等分線ｎです。

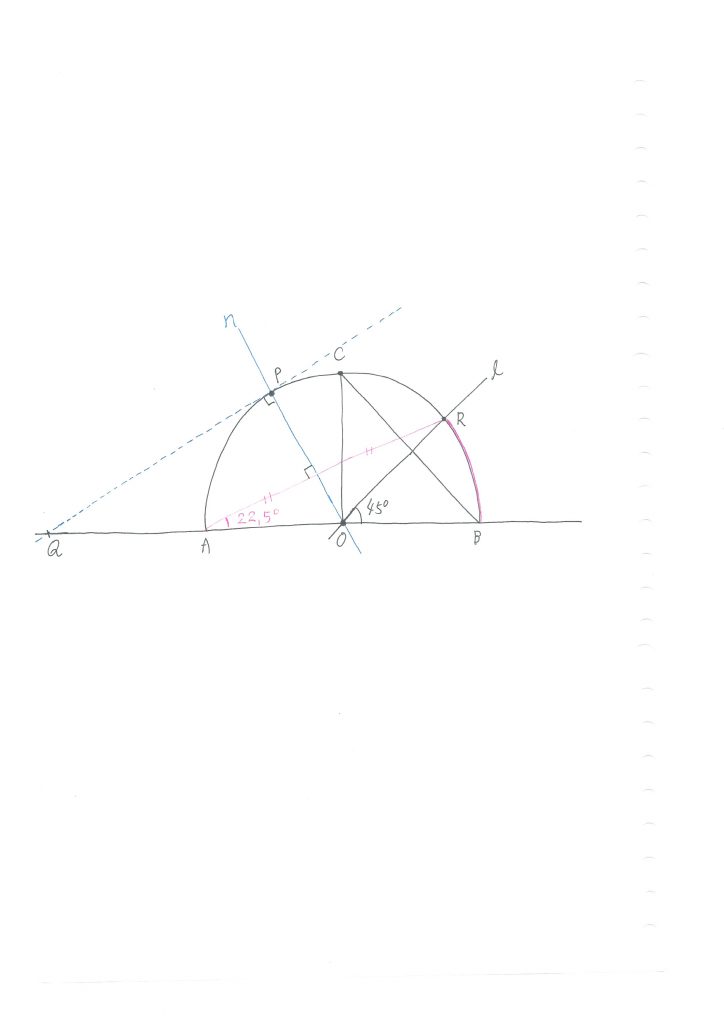
実は、直線ｎと半円Oとの交点が、求める点Pです。

理由は、良い問題だと思うので、少し考えてみて下さいね。

２次関数は、典型問題を当たり前に解ける練習を！

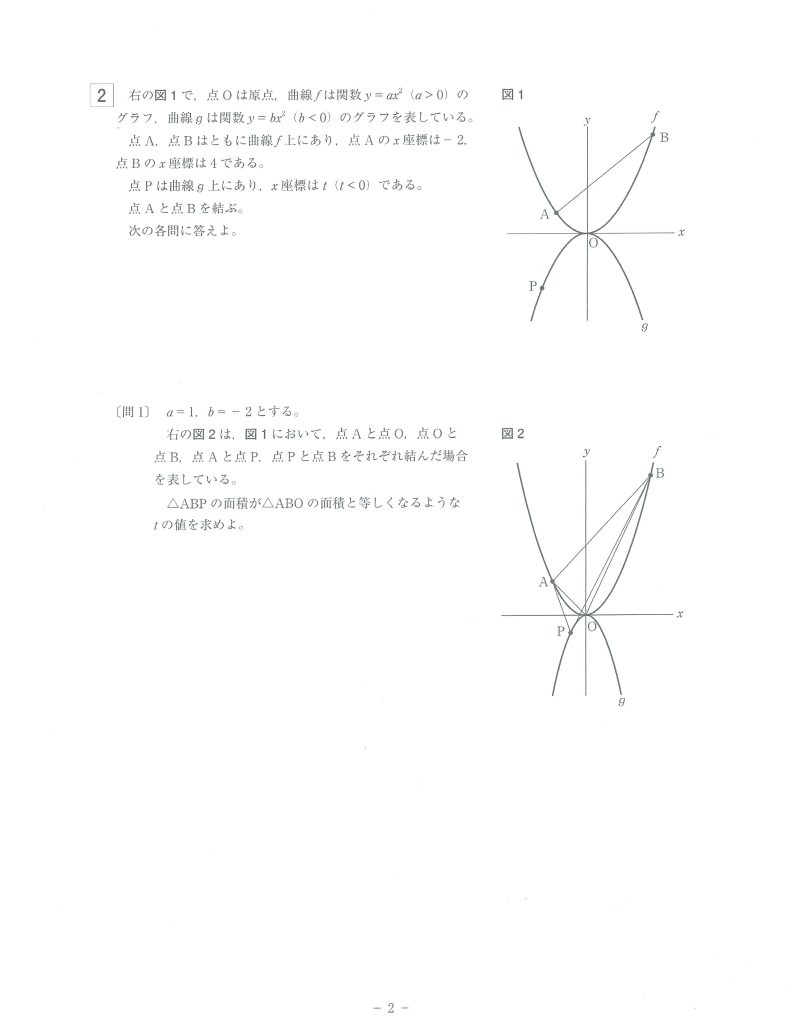
２次関数に関する問題は、面積の二等分や、グラフ上の点を結んで、線分の長さを求める問題など、どの問題集にも載っている問題を、当たり前に解ける力が求められます。

ここでも、曲線上にあって、面積が等しくなる点Pを求めることなど、典型的な問題を得点できるチャンスがあります。

ひとつひとつ見ていきましょう。

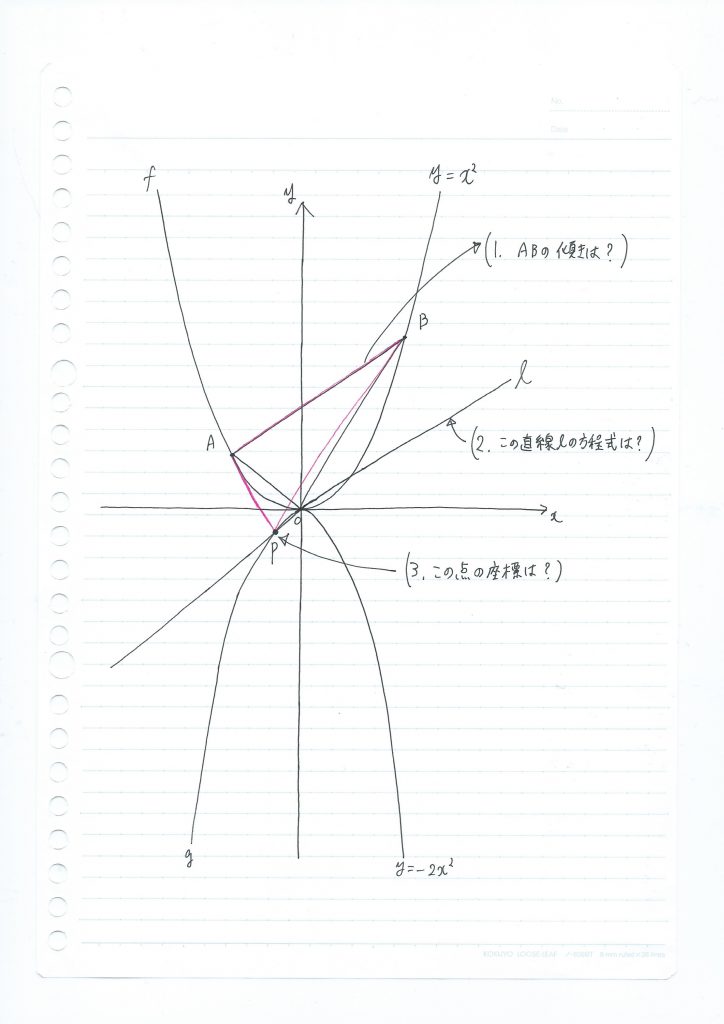
問１．「面積が等しい」ときたら等積変形

図から、△ABOと△ABPは、辺ABを共有していますね。

こういうときは、共有している辺ABを、底辺と見ることがお決まりの考え方です。

これ、なぜかというと、辺ABと平行で、原点Oを通る直線ｌが描ければ、その直線ｌと曲線ｇとの交点が、求めるべき点Pとなるからです。

なのでまずは、手順としては

１．直線ABの傾きを求める

２．直線ABと同じ傾きで、原点Oを通る直線ｌを求める

３．直線ｌと曲線ｇとの交点を求める

というステップを踏むことになります。

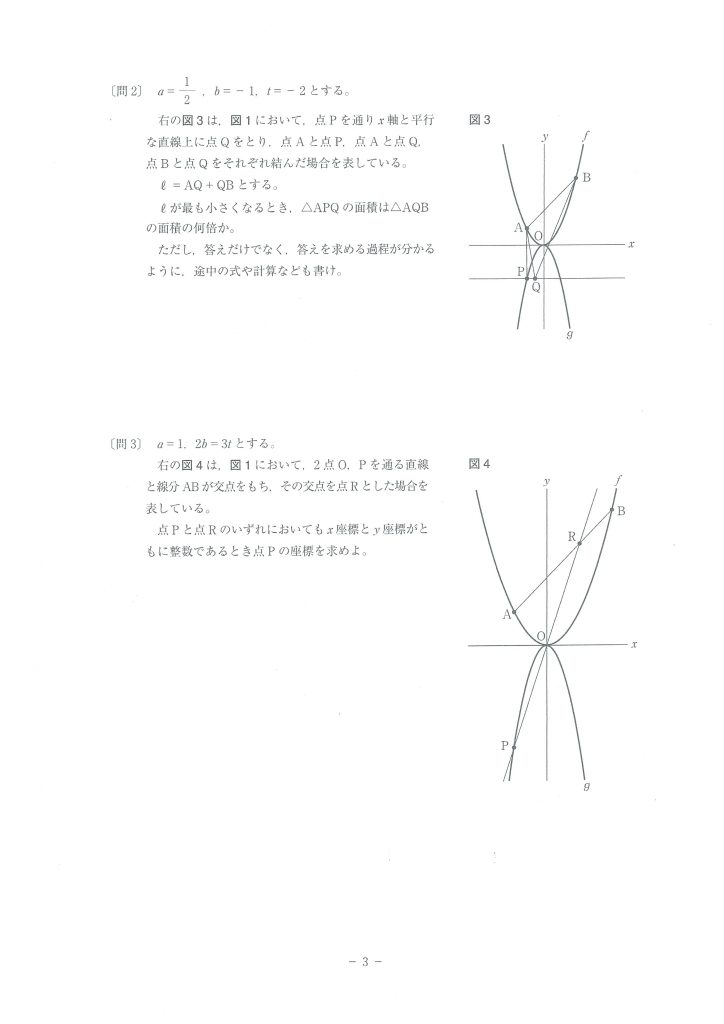
問２．「長さの和が最小」からは線対称な点を連想する

２点A、Bと、ある直線ｍが与えられたとき、直線ｍ上にある点Qのうち、その点Qと点A、点Bを結び、AQとBQの長さの和が最小になるものを探す問題です。

この問題の図を見ると、点Pを通りｘ軸と平行な直線をｍとすると、AP⊥ｍとなっています。

直線ｍに関して、点Aと対称な点をCとしましょう。

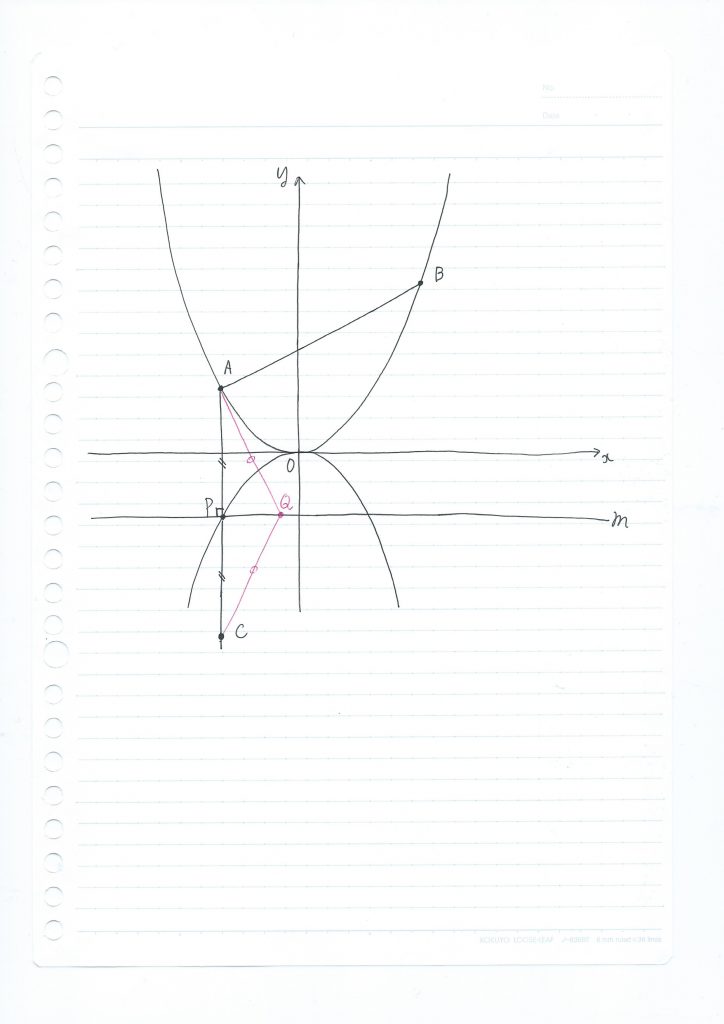
すると、△APQと△CPQは合同となるので、AQ＝CQとなります。

つまり、AQ+BQ＝CQ+BQです。

ここで、点Qを動かしてみますね。

すると、線分BQと線分CQは、折れ線を作るのですが、この折れ線の長さは、あるとき最小となります。

いつのことか、お分かりでしょうか。

３点B、Q、Cが一直線上に来たときです。

ですので、この問題の考え方は

１．点Pを通りｘ軸に平行な直線ｍに関して、点Aと対称な点Cの座標を求める

２．２点B、Cを通る直線BCの方程式を求める

３．直線ｍと直線BCの交点の座標が、求める点Qとなる

の３つがポイントとなります。

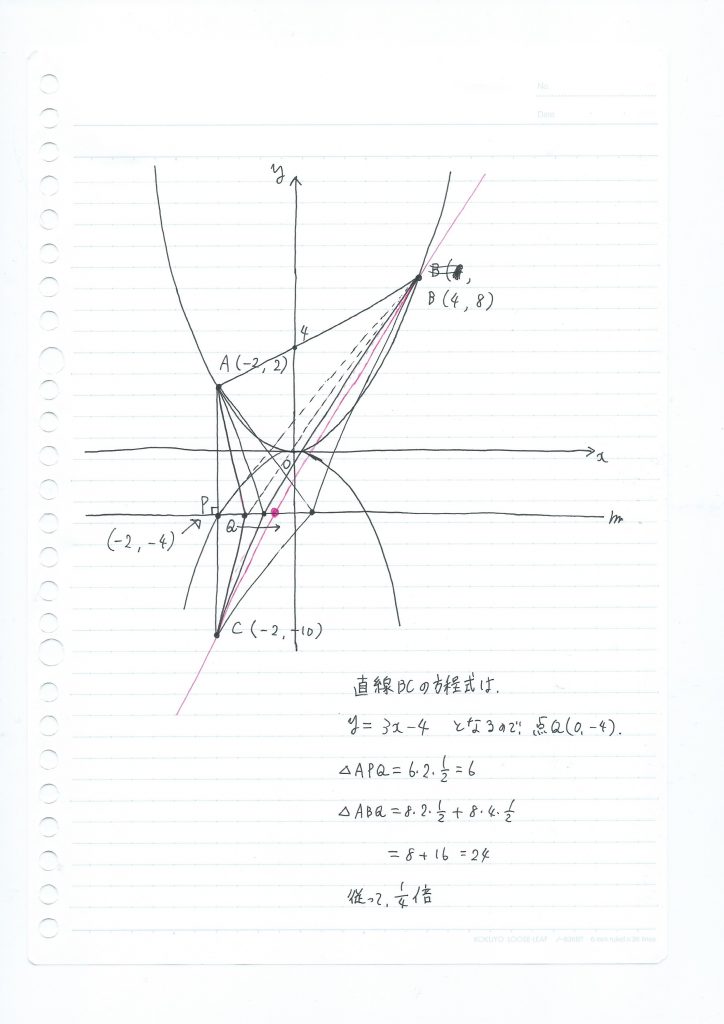
この考え方に沿って解くと

直線BCの方程式は、ｙ＝３ｘ－４、Q（０、４）

が得られ、△APQ＝６、△AQB＝２４となることが分かります。

この問題の問３はかなり難しい！

まずは、２ｂ＝３ｔを変形して、ｂについて解いて下さい。

すると、ｂ＝(３/2)tとなりますので、このｂをそのまま、ｙ＝ｂｘ＾２に代入しましょう。

曲線ｇの方程式は、ｙ＝（３/２）ｔｘ＾２となるので、点Pの座標を、ｔを使って表してみて下さい。

P（ｔ、（３/２）ｔ＾３）となりますね。

直線OPの方程式を求めて、直線ABとの交点を求めることになりますが、文字が２つ入ってくるあたり、計算テクニックや考え方が、中学数学の範囲を超える気がします。

直線OPの方程式・・・ｙ＝（３/２）ｔ＾２ｘ

直線ABの方程式・・・ｙ＝２ｘ+８

となるので、これらを連立して

ｘ＝１６/（３ｔ＾２－４）

を得ます。

問題文から、ｘ、ｔともに整数になるので

３ｔ＾２－４が取る値としては、１６の約数しか、あり得ないわけです。

つまり、３ｔ＾２－４＝１、２、４、８、１６

のみです。

この中で、３ｔ＾２－４＝８のとき唯一、ｔ＝２、－２という解が得られます。

そして最後に、ｔはどんな値だったか、確かめておいて下さい。

ｔは負の数です。

相似・合同・円の性質に関する問題

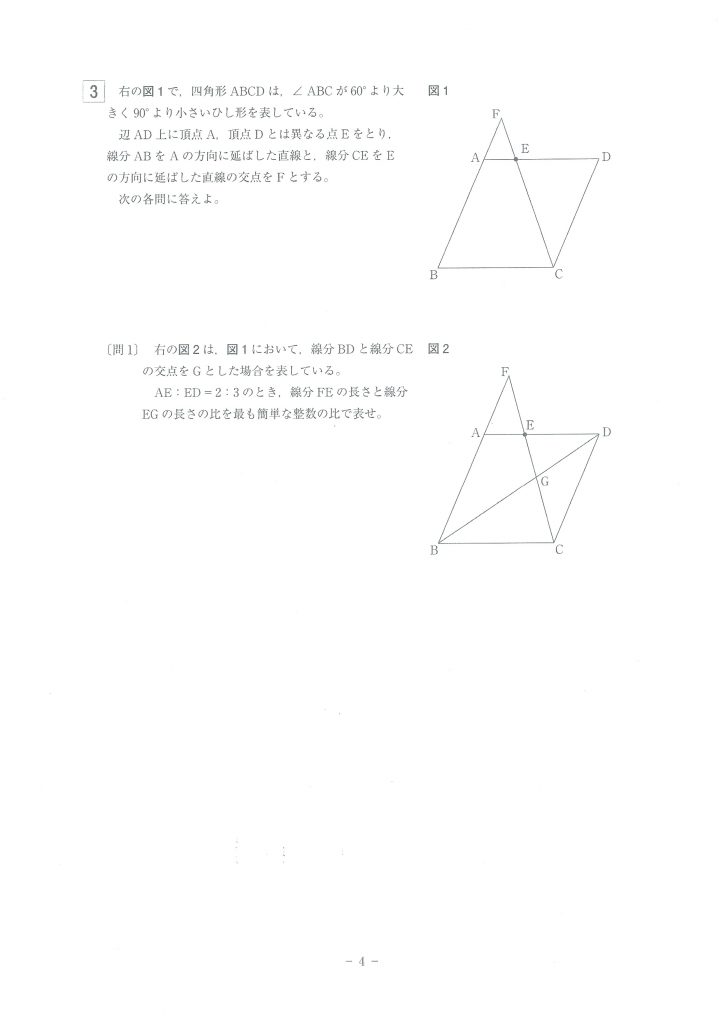
図形の問題は、相似や合同、円の性質など、全てを融合した上で出題される傾向にあります。

問１では長さの比を求めることになっています。

これは覚えておいてほしいのですが、長さの比を求める問題は、例外なく相似の知識を使います。

長さの比は、相似な図形を探すことから！

以下で、この問題のポイントを見ていきますね。

お互いに相似な図形は自分で探す

いま、問１では、AE：ED＝２：３とありますね。

そうしたらまずは、辺AEと辺EDを一辺とする三角形に注目して下さい。

辺AEを一辺とする三角形は、△AEF一つしかありません。

これに気がついたら、あとはやることはただ一つ。

△AEFと相似な三角形を探すことです。

見つかりましたか？

△DECです!

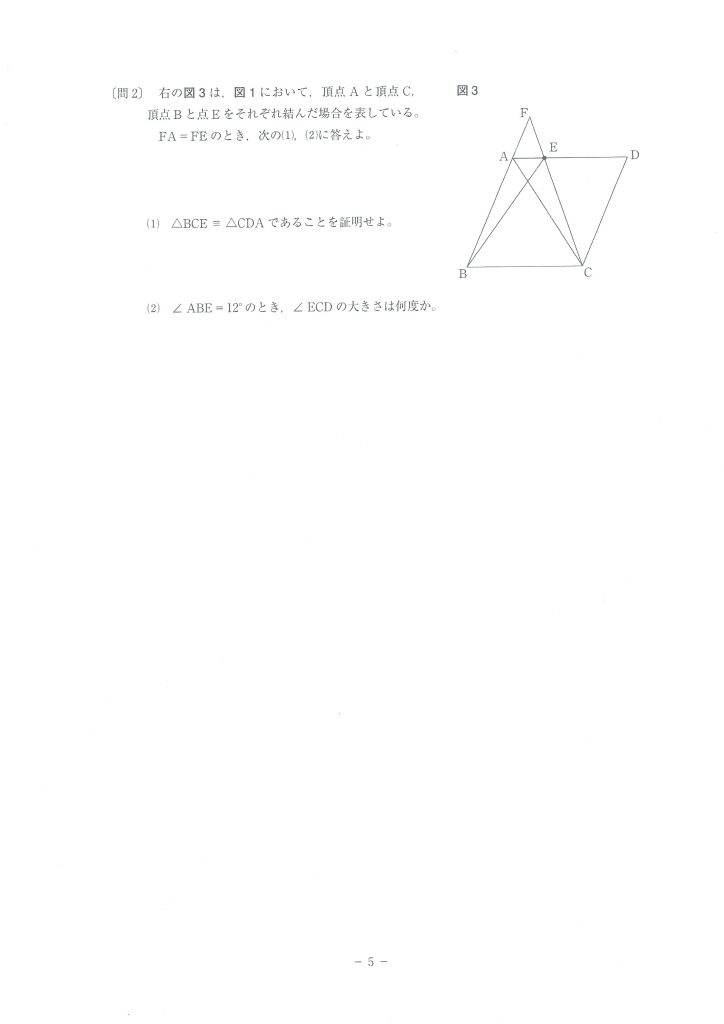
その相似比は、もちろん、２：３です。

ここで、そもそもどこの線分比を求めるのかを、確認しておきましょう。

私たちは今、FE：EGの比が知りたいのです。

ですので、次に考えることは、線分FEやEGと関係のありそうなところから、線分の比を求めていくことです。

辺EGは、辺EC上にあり、しかも△AEF∽△DECですので、とりあえずFE：ECは求まります。

FE：EC＝２：３となります。

一方向ではなく、多方向から図形を見る

FE：ECが分かると、後はどこが分かれば、FE：EGが分かるのか？

もう一度、図をよく見てみてほしいですね。

分かりますか？

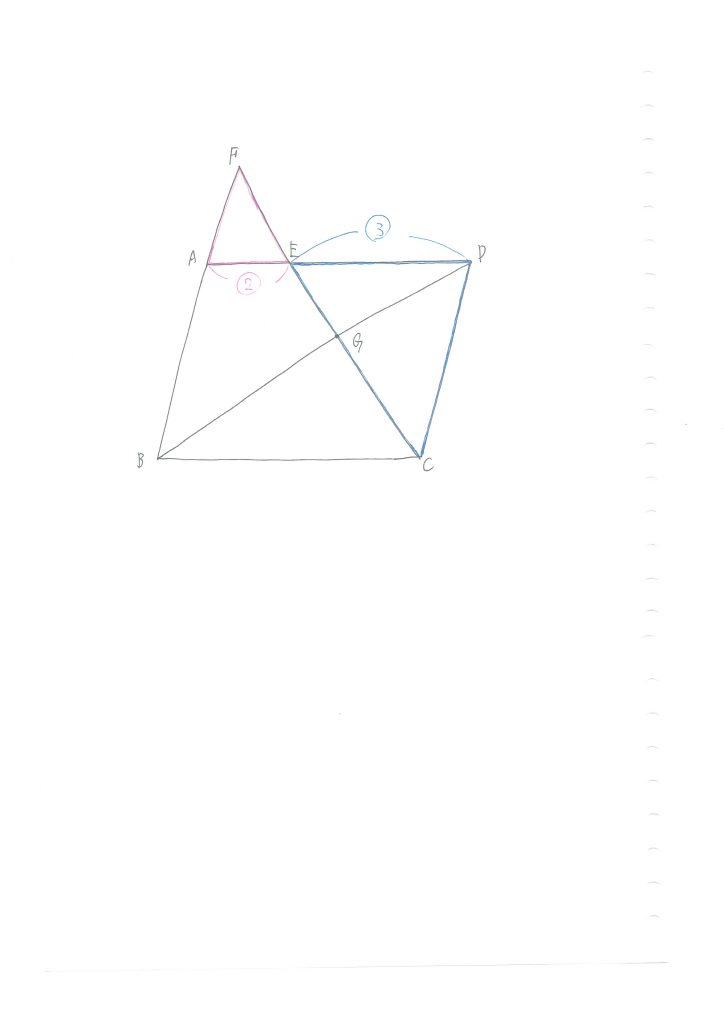
実は今度は、EG：CGを求めることで、FE：EGが分かるのです。

EG：CGを求めるためには、次は△EGDと相似な三角形を探すことになるのですが、もう分かりますね。

△EGD∽△CGBです！

相似比は、AE：ED＝２：３であり、比の値としては、ADの長さが５なので、BCも５になることから、EG：CG＝３：５となります。

比の値を２通りの見方で捉える

今、線分の比は

FE：EC＝２：３

EG：CG＝３：５

であることが分かりました。

これは、見方としては、EC＝３としたとき、長さ３のものが更に３：５に分けられているということです。

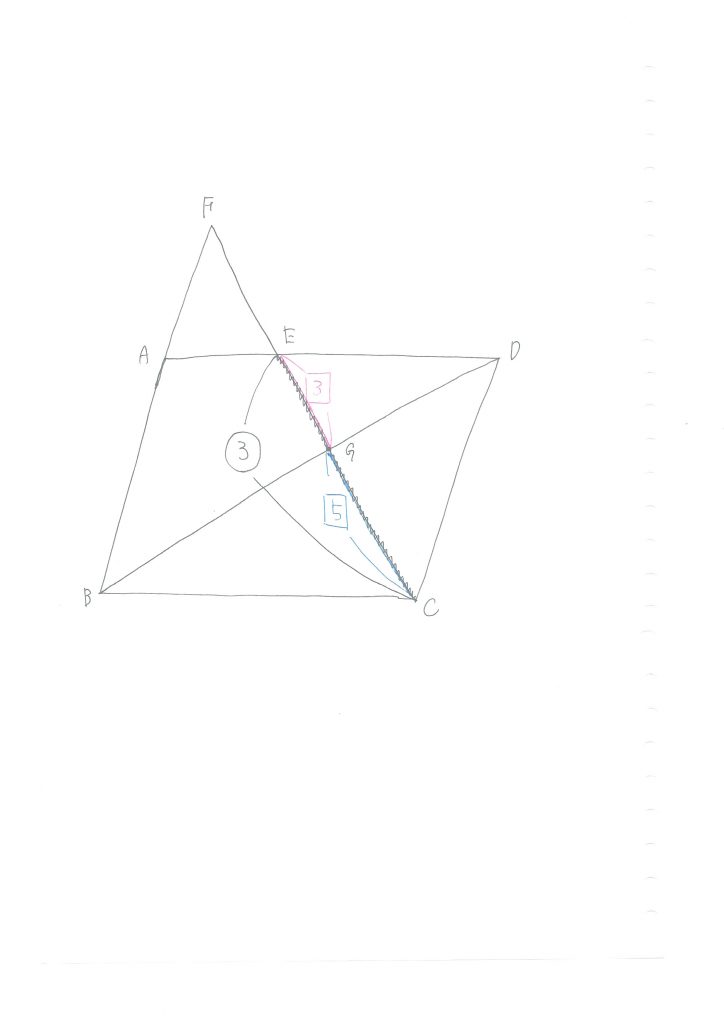
つまりは、EG＝３×（３/８）、CG＝３×（５/８）になるわけです。

このことから、やっとFE：EGが分かります。

FE：EG＝２：（９/８）

=１６：９

となります！

二等辺三角形においては、二辺が同じ以外にも大事なことが・・・

難しい問題をやっていると忘れがちなのが、問題では、どんな条件がついていたのかということ。

分からなくなりかけたら、もう一度問題文を読み返す！

これ、すごく大事です。

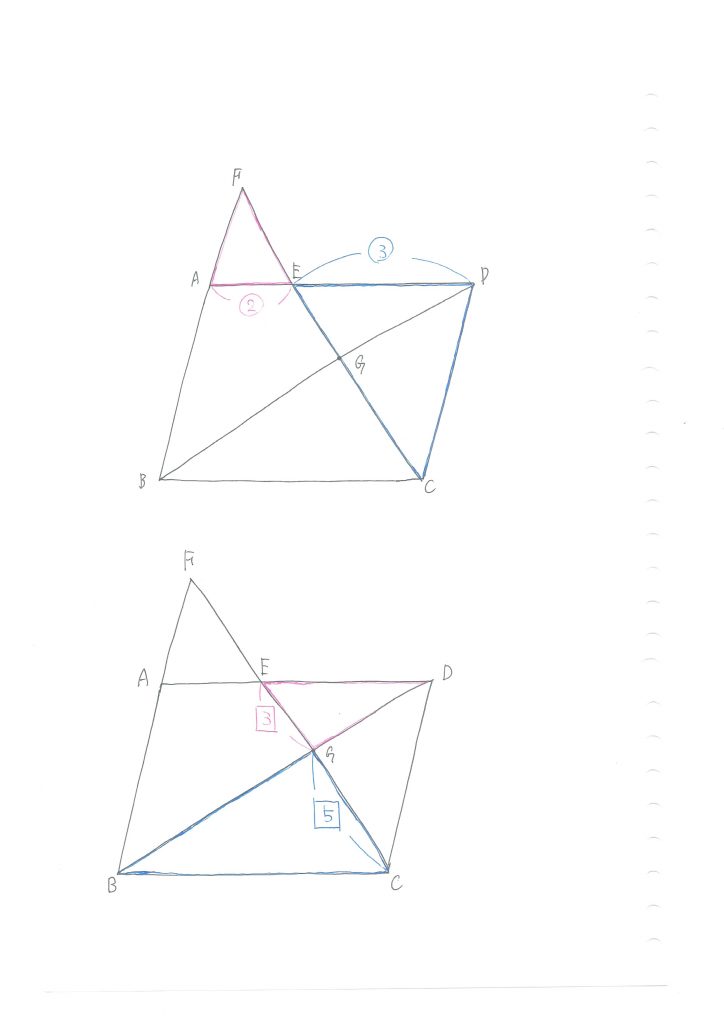
問題文をもう一度読むと、四角形ABCDはひし形とあります。

問２の（１）では、三角形の合同を示すわけですが、そのためにも、問題文にどんなことが書いてあったのかを確かめて、何が証明のヒントになるのかを、見つけていきましょう。

四角形ABCDはひし形なので、△BCEと△CDAにおいて、まずはBC=CDが分かります。

次に、FA=FEですから、△AFEは二等辺三角形なので、∠FAE＝∠FEAが分かります。

二等辺三角形ときたら、「二辺が同じ」だけではなく、「底角も同じ」ということが頭の中にあると良いですね。

この考え方、よく使います。

あとは、同じ角度を、どんどん探していきましょう。

三角形の証明問題は、同じ角度を探すことこそがポイントであると言っても良いでしょう。

∠FAE＝∠FEA・・・①

∠FAE＝∠ABC（平行線の錯角)・・・②

∠ABC=∠CDA（ひし形の対角は等しい）・・・③

∠FEA=∠ECB（平行線の錯角）・・・④

さて、これらをうまく組み合わせることで、∠BCE＝∠CDAが言えるのですが、お分かりですか？

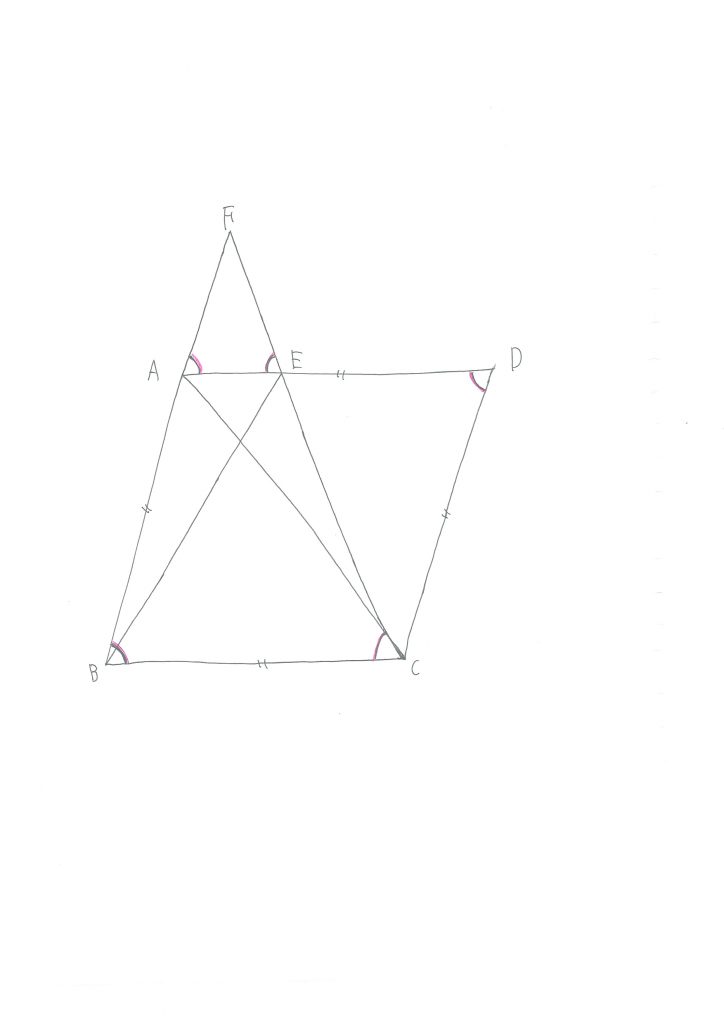
今分かったことは

BC=CD・・・（ア）

∠BCE＝∠CDA・・・（イ）

の２つなので、あと一つ、何かが言えれば良いのです。

そのヒントになるのは、やはり、二等辺三角形の底角は等しい、逆に、底角が等しければ、二等辺三角形になるということ。

あることに気がつけば、すぐにどの三角形が二等辺三角形になるのかが分かります。

∠FEA=∠DECですので、上の①～④と組み合わせれば、∠DEC＝∠CDEが言えて・・・。

三角形DECは、二等辺三角形となるので、CD＝CE

四角形ABCDはひし形なので、CD＝DA、つまり、CE＝DA。

CE＝DAと、上の（ア）と（イ）とを組み合わせて、△BCEと△CDAにおいて、二辺とその間の角度が等しいことが分かりますね。

角度について方程式を立てるという考え方

（２）でも、やはり底角が等しければ二等辺三角形になるという考え方は使います。

∠FBC＝∠CDA

∠BCE＝∠CDA(△BCEと△CDAが合同なので）

から、∠FBC＝∠BCEなので、△BCFは二等辺三角形となって、FB=FC。

さらにFE＝FA、∠AFEは共通。

△FEBと△FACは合同となるので、∠FCAも１２度になります。

ここまで分かったら、あとは、∠EBC＝aとおいて、角度に関する方程式を作ります。

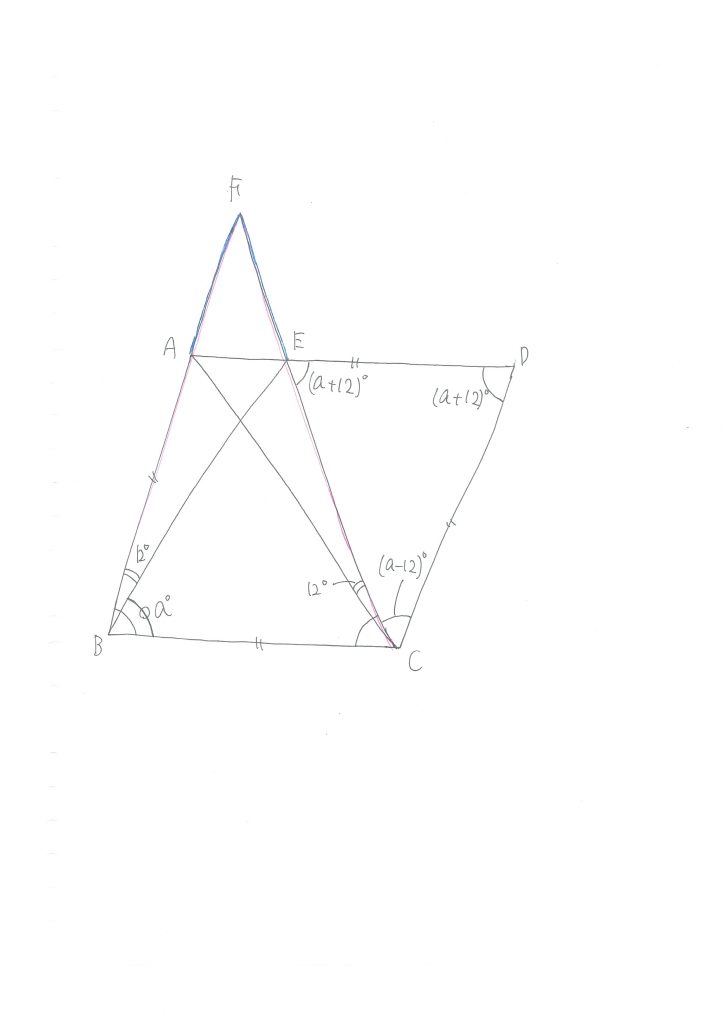
すると、

∠ABC＝a+１２

∠CDE＝a+１２

∠DEC＝a+１２

∠ECD＝a－１２(理由を考えてみて下さいね）

なので、これらを合わせて１８０度となるから

（a＋１２）＋（a＋１２）＋（a－１２）＝１８０

を解いて

a=56

つまり、∠ECD＝４４度となることが分かります。

三平方の定理と図形の計量

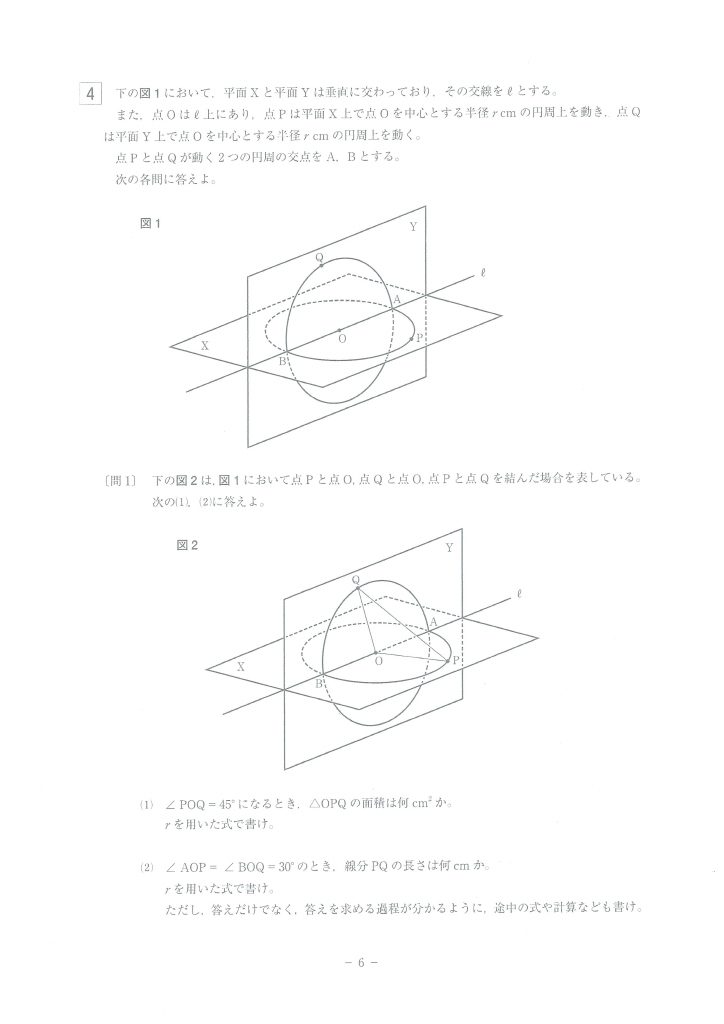
見た目難しそうですが、問題文を注意深く読み、自分で図に描き込んだりすることで、問題を解くためには何をすれば良いのかが、分かってくると思います。

空間ではなく平面で考える

この問題の問１では、各点が空間の中にある場合のことが問われています。

この図だと、△OPQが空間の中にいる感じが強すぎて、少し分かりづらいですね。

そういうときは、平面に落として考えてみましょう。

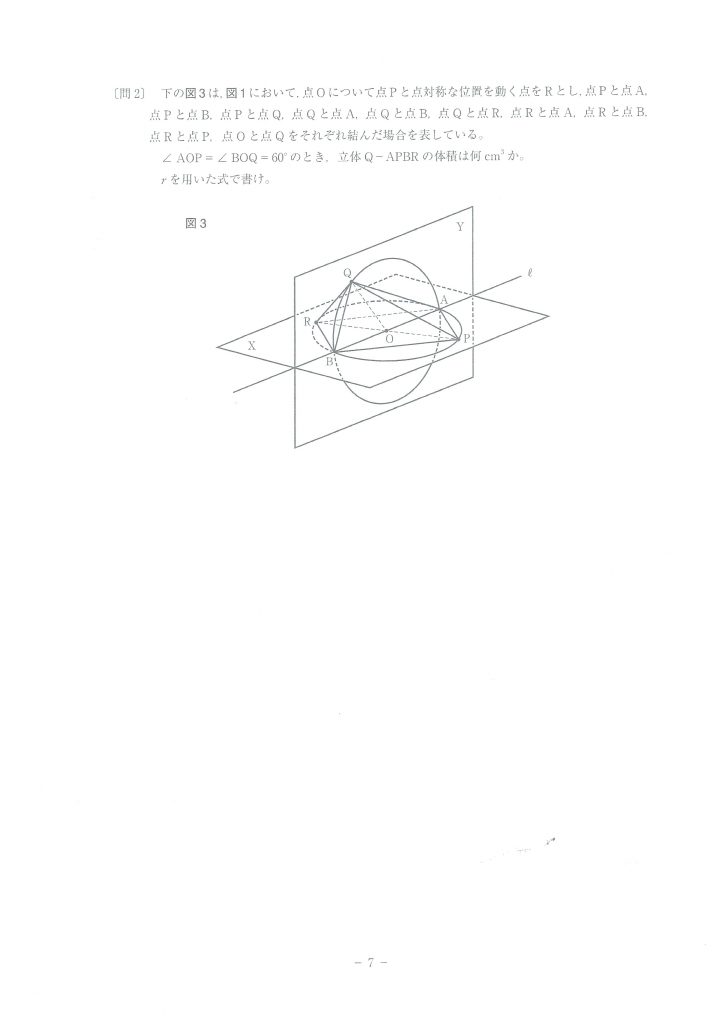
この図において、点Qから辺OPに垂線の足Hを下ろすと

OP＝ｒ、QH＝ｒ/√２

となるので、簡単に△OPQの面積が出ますね！

三平方の定理が使える図形を自分で作る

この問題は、私は少し悩みました。

どうやって解くのか・・・？

空間の座標を考えて、三角比が使えたらどんなに楽か（笑）

とも考えましたが、これは高校入試！

そんな技は、まだ使えません。

考え方としては

線分PQを一辺とする直角三角形を自分で作り、三平方の定理を使って、PQの長さを求める

ことが、この問題のポイントとなります。

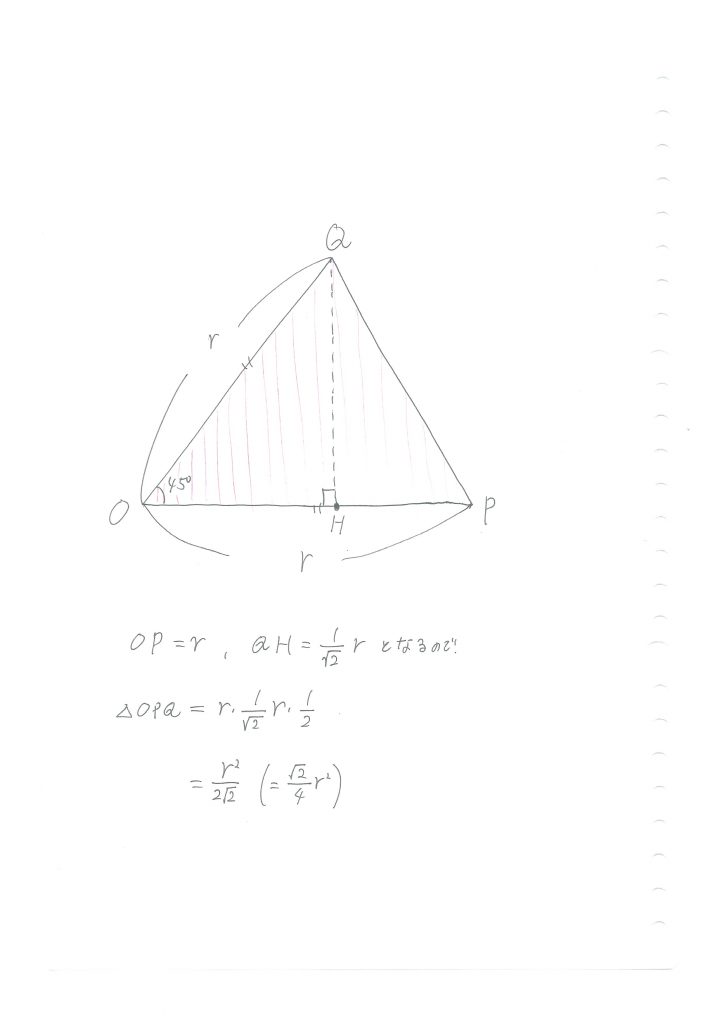
そのためにはまず、点Qから線分AB上に垂線の足Hを下ろしてみて下さい。

特別な直角三角形の辺の比を使いこなす

すると、△OQHは、辺の比が１：２：√３の直角三角形になっているのですが、お分かりでしょうか。

比の値で、２に当たる辺がOQですので、OQ＝ｒとなっていることから、QH＝ｒ/２、OH＝√３ｒ/２となっています。

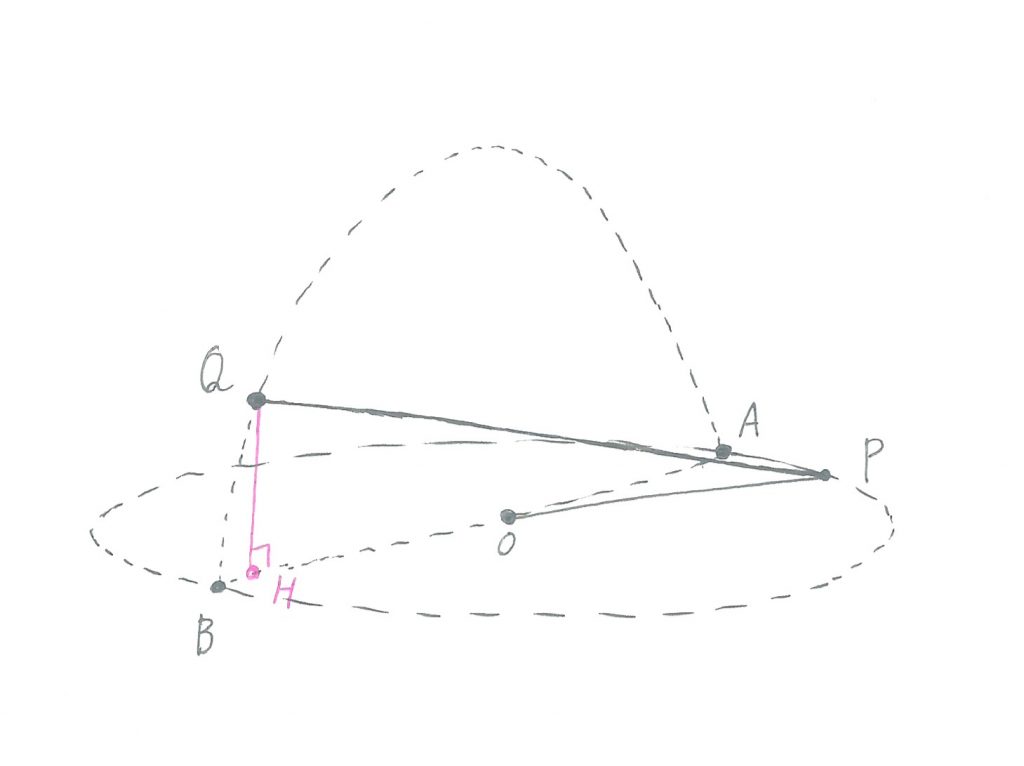
今度は、点Hと点Pを結んでみましょう。

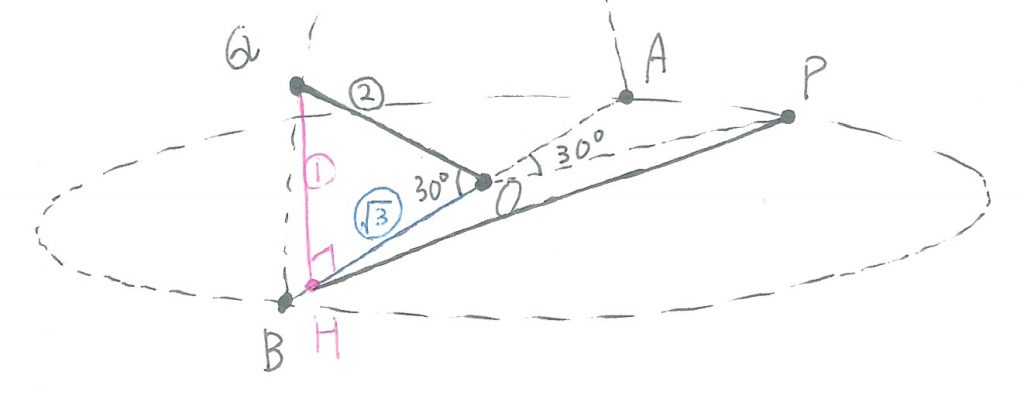
△PQHは、どんな三角形になっているか、分かりますか？

辺QHと、平面X上にある点Oを中心とする円Oは、垂直に交わっているので、△PQHは∠QHP＝９０度の直角三角形なのです！

そうしたら、あとは辺PHの長ささえ求めれば、辺PQの長さが分かります。

ここに図を載せておきますので、辺PHの長さが√１３ｒ/２になることを、確かめてみて下さい。

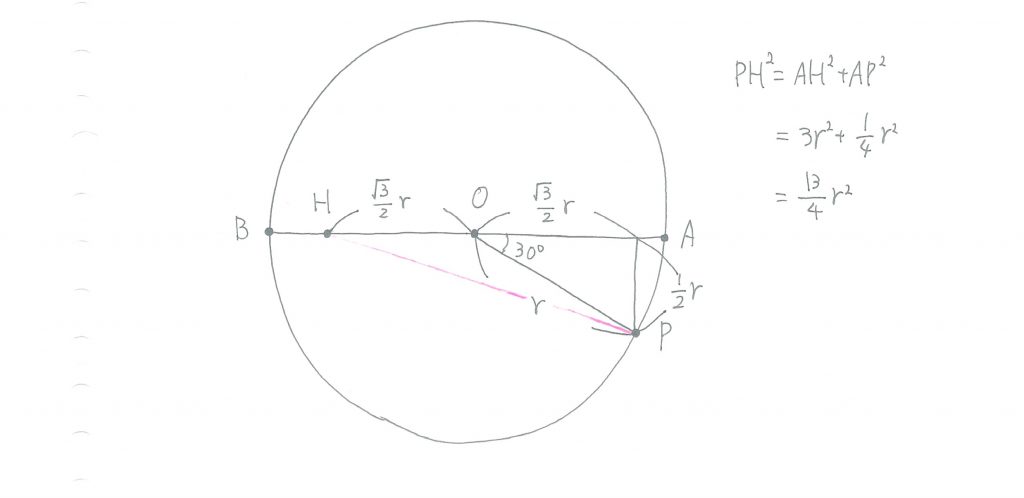
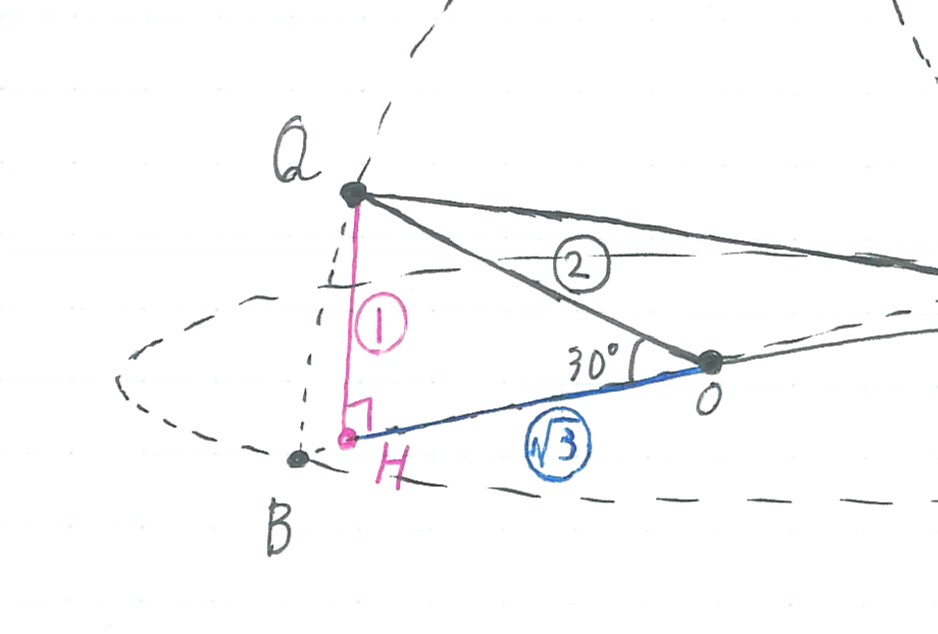
△PQHにおいて

QH＝ｒ/２

HP＝√１３ｒ/２

となるので、あとは三平方の定理を使って、辺PQの長さを求めてみて下さいね。

体積を求める前に、どんな立体になっているのかの確認を！

最後に、問２では、立体QーAPBRの体積を求めることになっていますが、そもそもこの立体、どんな形になっているのでしょうか。

５点O、A、P、B、Rの位置関係は、個別に描くとこんな感じですね。

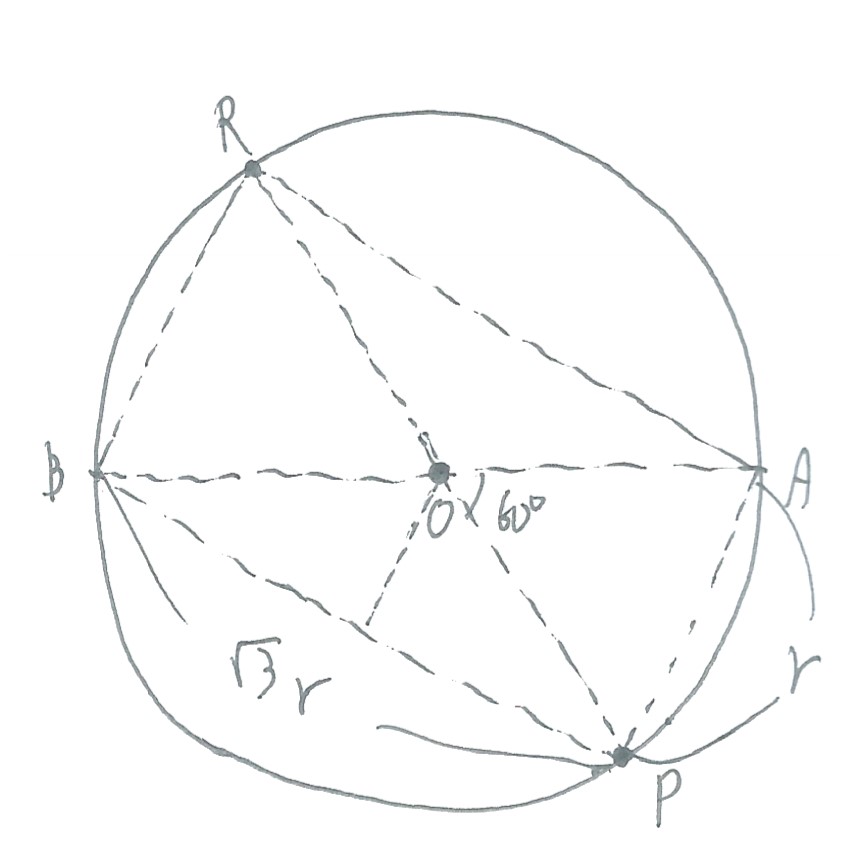
空間図形の問題では、平面での位置関係を個別に描いて考えることは、ものすごく大事ですので、ぜひやってみて下さい。

四角形APBRは、長方形です。

理由は、四角形APBRの全ての角が、平面X内にある円Oの直径に対する円周角になっているからです。

直径に対する円周角は、９０度です！

お忘れなく！

さて、四角形APBRの各辺の長さについてですが、∠AOP＝６０度というだけで、いろいろすぐに分かってしまいます。

AP＝ｒ

BP=√３ｒ

となっています。

四角形APBRの各頂点と、点Qが結ばれて、立体ができあがっているのですが、実はこれ、四角すいなのです！

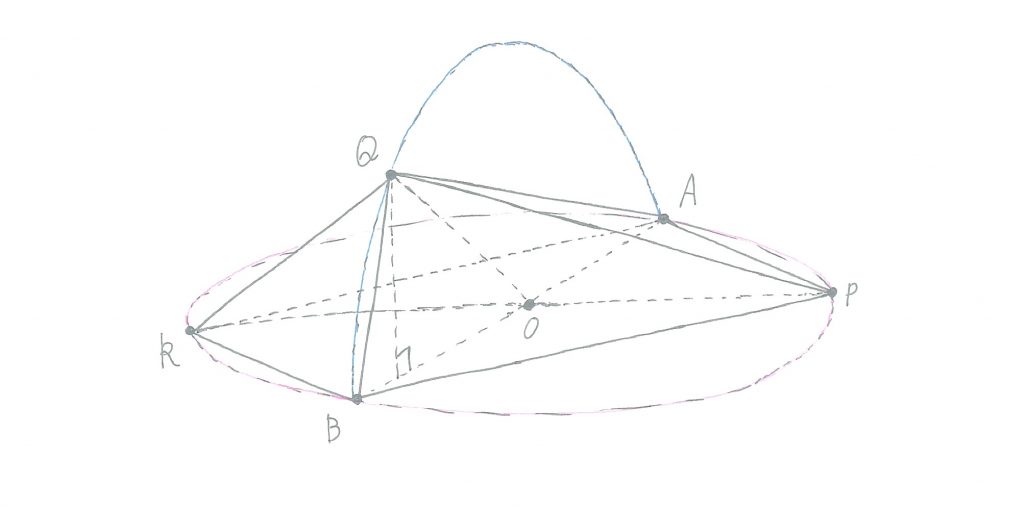
上の図で、例えば点Qが点Oの真上にあれば、すぐに四角すいだと分かる人も多いのですが、この問題では、∠BOQ＝６０度となるところに、点Qがいるのです。

少し豆知識になるのですが、空間内に、何か変な平面図形Xと、X上にない別の点Pが与えられたとき、点Pと図形Xのまわり(境界線）の各点を線分で結んでできる立体図形を、すい体(cone）といいます。

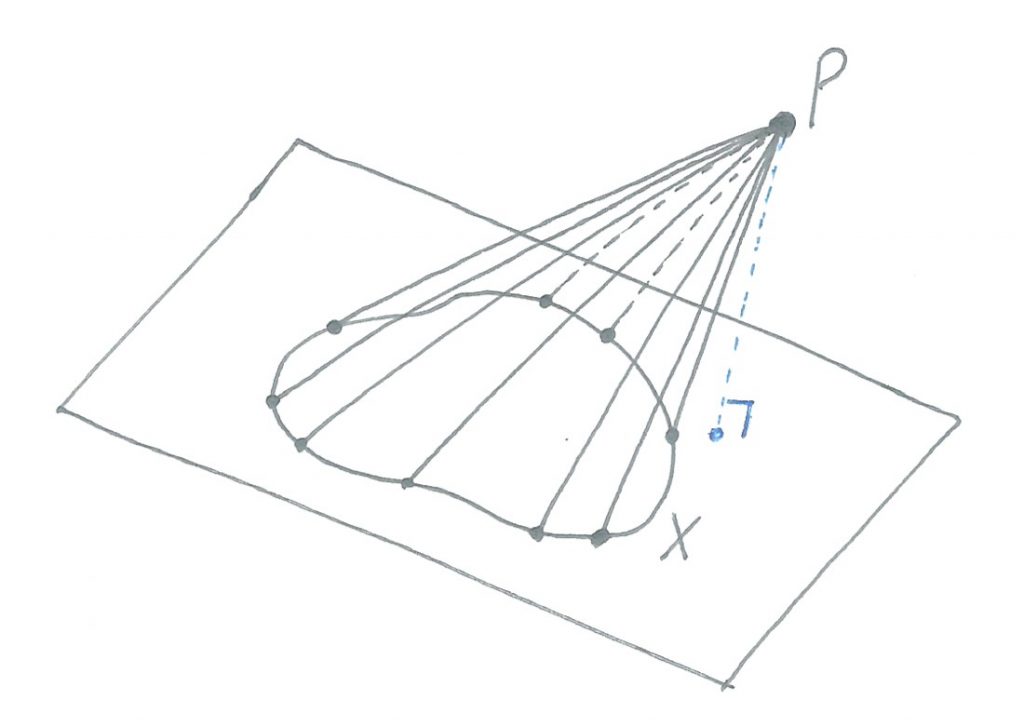
そして、面白いことに、この立体の体積は

（図形Xの面積）×（点Pから図形Xを含む平面に下ろした垂線の長さ)×（１/３）

で求められるのです。

ですので、この問題の問２の場合も

体積＝(四角形APBRの面積)×(点Qから下ろした垂線の長さ)×(１/3）

で求められます。

点Qを△ABQの頂点の一つとみると、△ABQは、平面Xと垂直に交わっているので、点Qから辺ABに垂線の足Tを下ろすと、線分QTの長さが、そのまま四角すいQーAPBRの高さとなります。

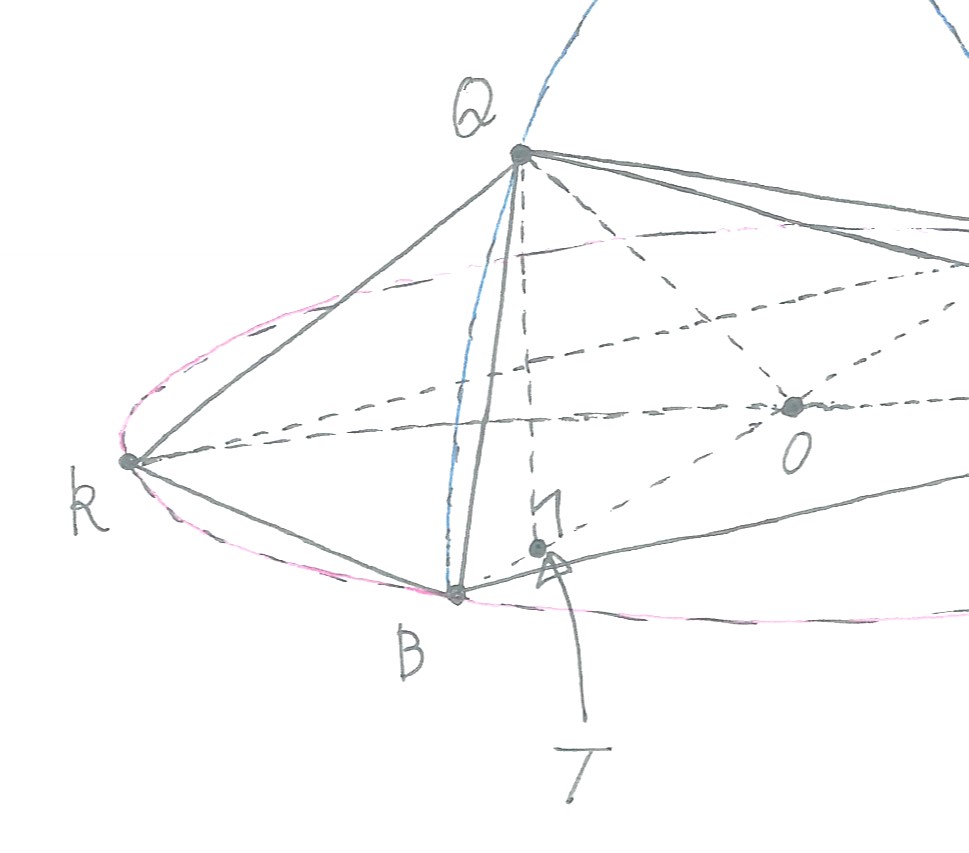
∠BOQ＝６０度ですので、またまた特別な直角度三角形の辺の比から

QT＝√３ｒ/２

となります。

これで、体積が求まります。

まとめ（来年度への対策)

問題を一つ一つ見ていくと、与えられた図が少し複雑であるとか、問題文を理解することが難しそうといった印象も、あるかもしれません。

全ての問題への、共通の対策として言えるのが、ものすごい計算力を付けておくことは、最も大事です。

もう少し具体的に言うと、長く、複雑な計算があったとしても

こんな風に計算すれば見通しが良くなるのではないか？

と自分で仮説を立てながら、いかにして、難しいと感じる計算であっても、自分で基本的なことにまで、戻って考える力が求められます。

こうした力は、どの問題でも求められます。

今から対策を考えている方は、教科書の問題を、何もヒントを与えられることなく、自分で解けるまでこなすことが大事です。

参考までに、体系数学の教科書(１、２)を挙げておきます。

この教科書は、私立の中高一貫校などで使われていますが、難関高校の受験を考えるのであれば、手にしておきたい一冊です。

ここに載っている例題とその類題を、全て解くことができれば、十分に対策していける力は身についてくるでしょう。

それができたら、まずは過去問を見て、解いていくことが先です。

数学の対策は、過去問に始まり、過去問に終わる

この前提に戻りましょう。

過去問をやってみて、問題の中で問われている考え方や、求められている解き方と、だいたい同じ解き方で解ける問題を、また別の問題集の中から探し、練習していくことが、一番の対策になります。

この記事も、参考になれば幸いです！