こんにちは。算数・数学専門家庭教師の鈴木です。
今日は女子学院中学校の算数入試問題の大問5番についての記事を書いていきます。
過去に大問1から大問4までの記事を書いておりますので、そちらもお読みいただき、参考にしていただければと思います。
↓大問1の解説はこちら↓
【女子学院中学校2022年算数入試問題】大問1を問題ごとに徹底解説 傾向と対策もアドバイス – 算数・数学オンライン個別指導塾 等々力・自由が丘プロ家庭教師 (sugaku1bann.com)
↓大問2の解説はこちら↓
【女子学院中学校2022年算数入試問題】大問2を問題ごとに徹底解説し、傾向と対策もアドバイス – 算数・数学オンライン個別指導塾 等々力・自由が丘プロ家庭教師 (sugaku1bann.com)
↓大問3の解説はこちら↓
【女子学院中学校2022年算数入試問題】大問3を問題ごとに徹底解説! 傾向と対策もアドバイス – 算数・数学オンライン個別指導塾 等々力・自由が丘プロ家庭教師 (sugaku1bann.com)
↓大問4の解説はこちら↓
【女子学院中学校2022年算数入試問題】大問4を問題ごとに徹底解説! 傾向と対策もアドバイス – 算数・数学オンライン個別指導塾 等々力・自由が丘プロ家庭教師 (sugaku1bann.com)
今回解説する問題がこちらです。
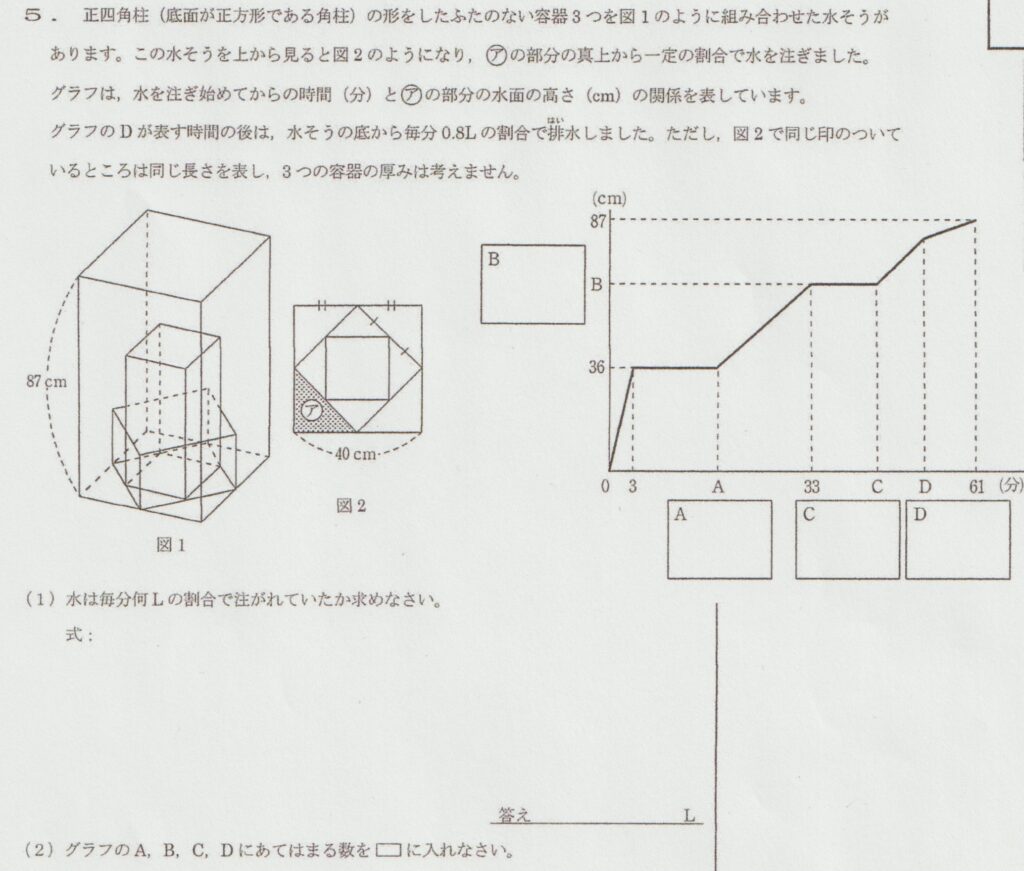
ポイントは「水がどのように流れるのか」を考えること
この問題の場合、㋐の部分に水を入れるのですが、㋐に水がたまってからどのように水が流れていくのかを考える必要があります。
水の流れを分かりやすくするためにも、以下のように、水がたまる領域を㋑から㋗の8つに分けて考えてみました。
各領域に水が流れるとき「等分されて流れる」と考える
㋐に水がたまった後は、㋑から㋔の領域に同時に水が流れ出しますが、ここでは「それぞれの領域に同じ分ずつ水が流れる」と考えます。
つまり「どこかの領域に偏って水が流れることはない」ということです。
このような考え方をもとに解説したものがこちらです。
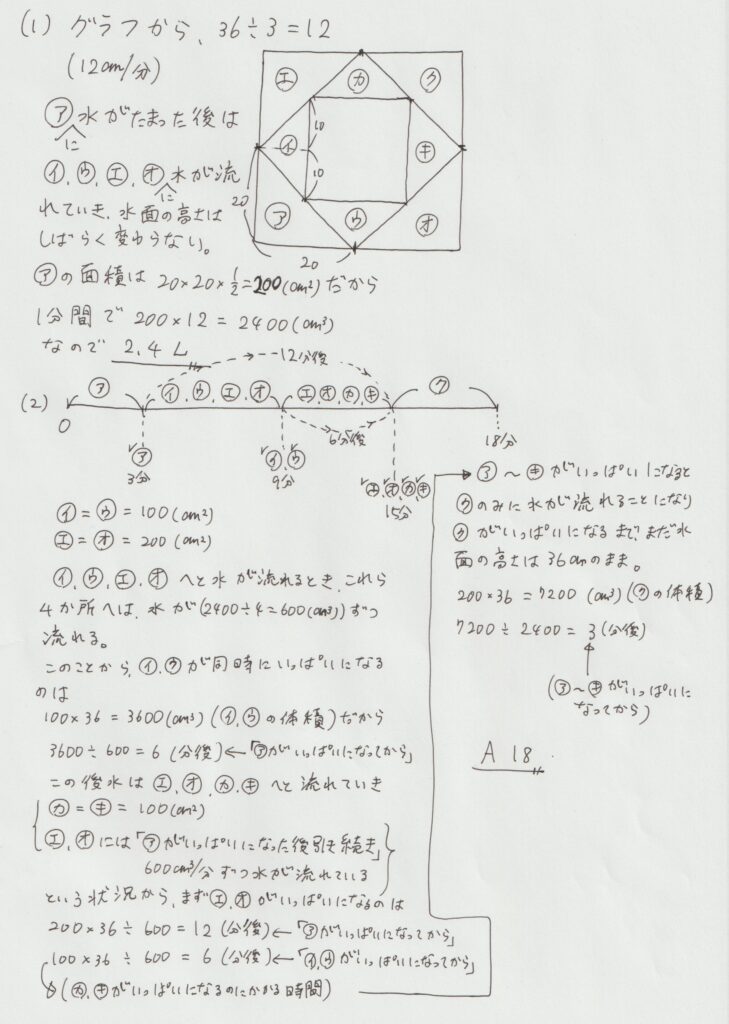
大事なことは「体積=底面積×高さ」
「底面積がいくつで、高さがいくつになれば良いのか」を考えることが、体積を出す上で必須です。
この問題も例外なく、そのようなことを繰り返し考えていきながら正解を出すことになります。
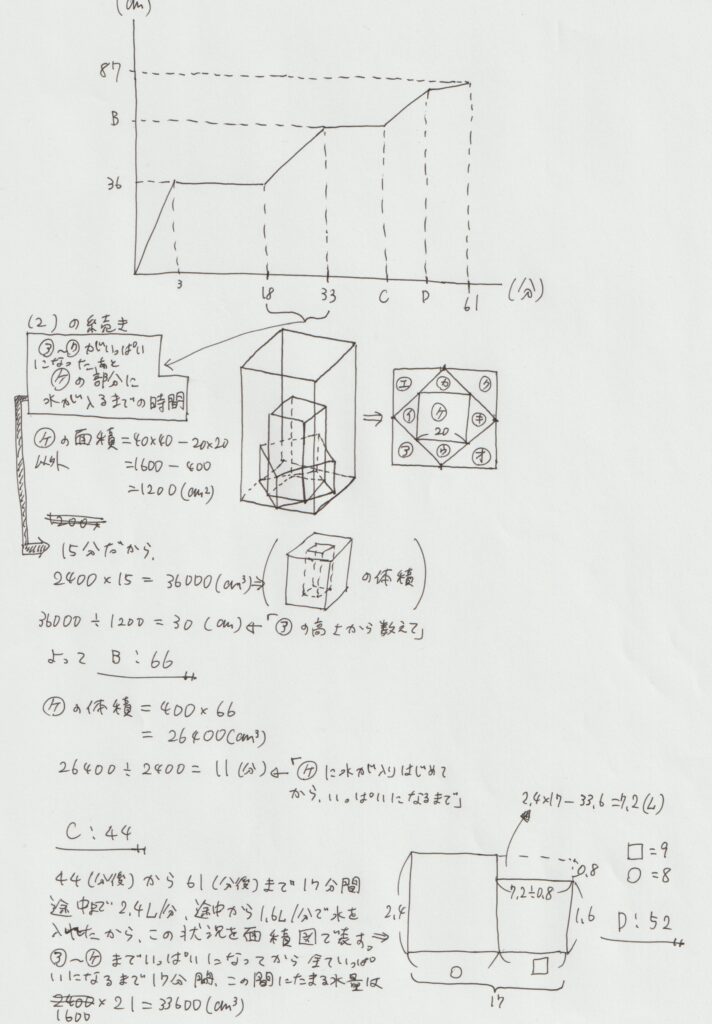
最後は「つるかめ算」で正解できる
問題文に「グラフのⅮが表す時間の後は、水そうの底から0.8 Lの割合で排水しました」とありますよね。
ですのでⅮの値を求める際に、問題文はこのように言い換えられます。
「水を入れ続けた17分間のうち、途中まで毎分2.4 L、途中から毎分1.6 Lで水を入れ続けたらたまった水量が33.6 Lとなったとき、毎分2.4 Lで入れ続けたのは何分間か?」
このような考えを面積図で表すことができると正解できます。
まとめ
典型的な問題ではあるものの「水がどのように流れるのか」を考えることや、「自分で基本的な問題設定に直すこと」が必要な問題です。
まずはどんな中学でも出ている「典型的な入試問題」をできるようにしておくと、この問題もできるようになりますので、ぜひこの解説も参考にしてみて下さいね。
