都立日比谷高校の数学の対策を、どのように立てていますか?
記事のタイトルには「過去問」とありますが、「いきなり過去問に手をつけることはできない!」と思う方も多いのではないでしょうか。
確かに過去問を解くことで、出題傾向を把握し、自分の得意不得意を見つけることはできますよね。
ただ、過去問を解き「できなかった問題と似たような問題」が本番で出てきたときに、できるようにしておくためにはどうすれば良いのでしょうか。
この記事では、このような疑問に答えるべく、都立日比谷高校の数学の過去問の解答例と対策を徹底的に解説します。
具体的な問題の解き方だけでなく、問題の背後にある出題意図や、それに対する最適な対策方法についても詳しく説明します。
一緒に、日比谷高校の数学の過去問題を解き、理解を深め、受験対策を強化しましょう。
都立日比谷高校の数学 過去問の特徴と傾向

まず、数学の過去問の特徴と傾向を理解することで、受験生が試験に向けての対策をより具体的に行うことが可能になります。
このセクションでは、都立日比谷高校の数学過去問の出題形式、難易度、出題範囲について詳しく解説します。
これらを把握することで、受験生は自身の学習計画をより効果的に立てることができ、試験に自信を持って臨むことができます。
入試問題の出題形式
都立日比谷高校の数学の入試問題は、大問4つから構成されています。
大問1は小問集合、大問2は関数とグラフ、大問3は図形と証明、大問4は空間図形という具合に、大問ごとに特定のテーマから出題されることになっています。
例年、大問2では二次関数、大問3では円の問題が必ず出題されています。
大問1は答えだけ、大問2から4については1問だけ記述式問題が出題されています。
この形式を理解することで、受験生は「どの単元のどの問題で得点すべきか」、また「問題を解く時間配分をどのように計画すれば良いのか」を知ることができます。
都立校独自の出題形式
また、日比谷に限らず、どの都立校でも言えるのは「図1」が与えられた上で「図2」ではどのような条件のもとに問題を考えていくのかが問われています。
例えば、以下のような問われ方の問題が、毎年必ず出題されます。
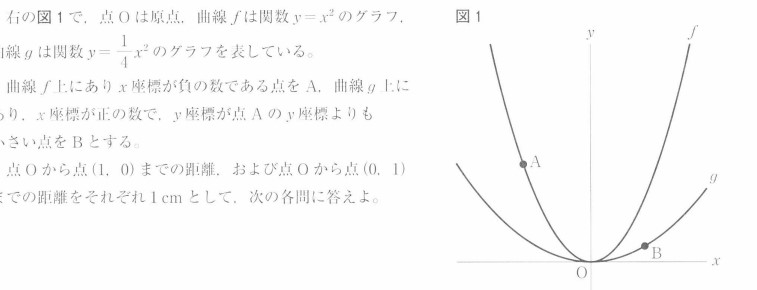
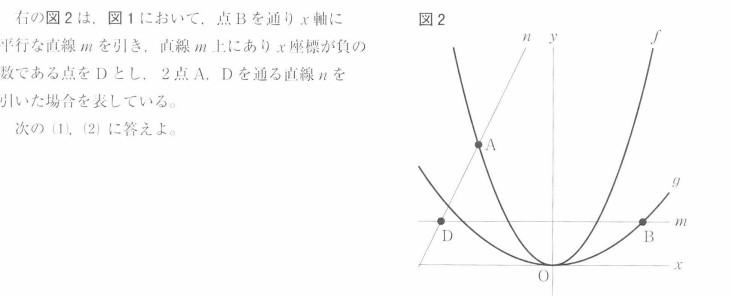
これはつまり「図1の条件を保ったまま、図2ではどのような条件のもとに、問題が出題されているのか」を把握する力が求められています。
このようなことを把握できるだけの「問題文を読む力」を、「過去問を題材として身につけること」が、都立入試の一番の特徴です。
入試問題の難易度
都立日比谷高校の数学の入試問題は、全体的に難易度が高い傾向にあります。
しかし、それぞれの大問においては、特に大問1の(1)番は「教科書レベルの基本問題に帰着される問題」が必ず出題されますので、ぜひ得点できるようにしたいところです。
この事実に加えて、大問1の小問は、どの高校受験向けの問題集にも載っているような「典型的な計算問題」が出題されます。
難易度は高いものの、まずはこのような「確実に得点できる問題」があることに注目しましょう。
入試問題の出題内容
都立日比谷高校の数学入試問題は、主に中学2、3年の数学の全単元が「融合問題」として出題されます。
融合問題とは言え、「二次関数のグラフと三角形」「円周角と相似な図形」「三平方の定理と角柱の体積」などなど「難関高校の入試問題としての定番」が出題されます。
以下に、それぞれの年度における2年分の出題データを紹介します。
令和5年度の出題内容
【大問1】
・問1. 平方根の計算
・問2. 二次方程式の解
・問3. 一次関数の変域
・問4. カードと確率
・問5. 円と作図
【大問2】
・二次関数のグラフと相似な図形
・二点を通る直線
【大問3】
・円周角と中心角
・合同な三角形と証明
・相似な三角形と辺の比
【大問4】
・中点連結定理と二等辺三角形の性質
・直角三角形の相似と三平方の定理
・すい体の体積
令和4年度の出題内容
【大問1】
・問1. 平方根の計算
・問2. 二次方程式の解
・問3. 一次関数の変域
・問4. 硬貨と確率
・問5. 半円と作図
【大問2】
・二次関数のグラフと直線
・三角形の面積
【大問3】
・円弧と中心角の関係
・直径に対する円周角と相似
・相似な三角形と辺の比
【大問4】
・相似な三角形と三平方の定理
・すい体の体積
問題を解くためのポイント
実際に私が解いてみた感想も交えてお話すると、二次関数であれ空間図形であれ「自分で相似な三角形を見つける」というポイントが、どの問題にも共通しています。
このポイントを意識した上で、今度は各問題の解答例を紹介します。
都立日比谷高校数学過去問の解答例と解説

大問1:小問集合の解答例と解説


日比谷としては易しいレベルの問題です。
例年、表を書いて解くタイプの問題も頻出ですので、樹形図を基本として解く習慣を身につけたいところです。


この問題の場合「30°」とあるので、どこかに60°を作れば良いという考えになります。
線分BCを正三角形の辺と捉えると、上の図のように正三角形BO’Cを作ることができ、「60°」を作ることができます。
点O’は、まずコンパスの針と芯の間隔を一定に保ち、針を点Bと点Cにそれぞれ合わせて円弧を描いたときの「円弧同士の交点」として得られます。
さらに、O’を中心として点Bと点Cを通る円を描けば、「∠BO’C=60°」をこの円の中心角と捉えることができます。
ですので、O’を中心とする円と与えられた半円の交点をPとすれば、「円周角と中心角の関係」から、∠CPB=30°となります。
大問2:二次関数の解答例と解説
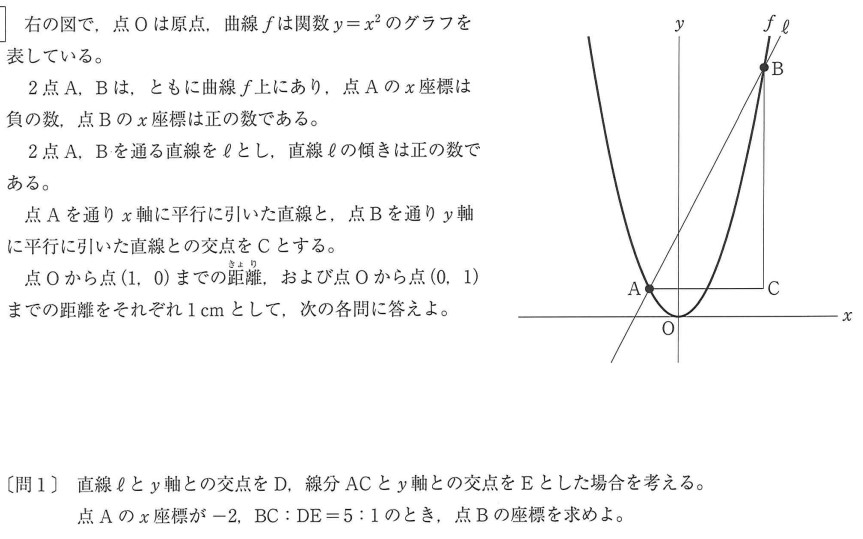

上の図で、△AED∽△ACBなので、点Cの座標は (8,4) 、点Bの座標は (8,64) となります。
二次関数の問題ですが、ここで早速「相似な三角形を見つける」という場面が出てきます。
大問3:円と図形の解答例と解説
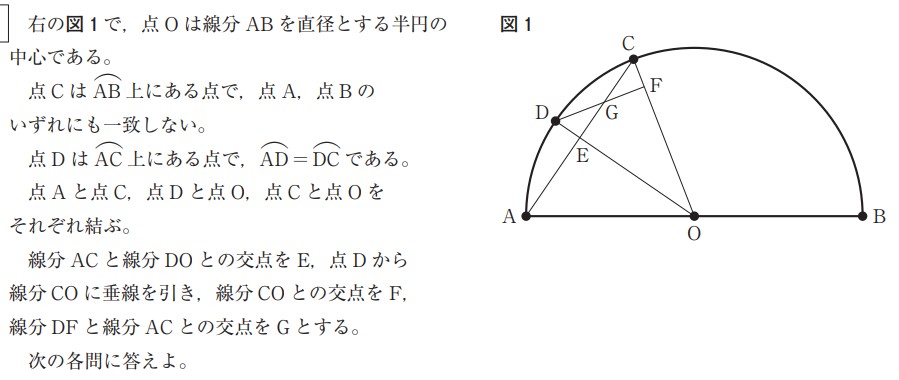


この問題を解くにあたり、∠GED=90°となることも、「弧の長さがお互いに等しければ、それらの弧に対する中心角も等しい」という円の性質を使い、△OAE≡△OCEを示すことで分かります。
基本的な円の性質は、問題を解く中で必ず出てきます。
大問4:空間図形の解答例と解説

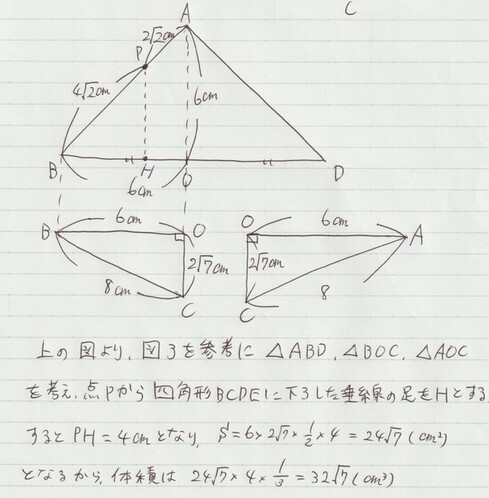
上の図で、線分PHの長さを出す際にも、△PHB∽△AOBに注目する必要があります。
このように、大問2から大問4では、必ずどこかしらで相似の考えを使います。
これも日比谷高校の数学の特徴です。
都立日比谷高校の数学 過去問対策と勉強

このセクションでは、中学1年生から受験直前までの段階別の対策と勉強法を詳しく解説します。
これを読むことで、自分の学習計画をより具体的に立てることができ、効率的に学習を進めることが可能になります。
さらに、適切な対策と勉強法を知ることで、過去問の使い方も分かり、入試本番において自信を持って問題に挑むことができるようになります。
中学1年生時の対策
中学1年生のときは、まず何よりも全ての単元の問題に「ミスなく正解できるようにしておくこと」が大事です。
例えば計算問題であれば、式の中に「中カッコ」まで含むような「累乗を含む正負の数の四則混合計算」「分数を含む文字式・方程式の計算」などは、必ずできるようにしておきましょう。
都立高校を狙う場合、方程式の文章問題は出題されないので、そこまで力を入れる必要はないものの、どの問題集にも載っているような文章問題は、できるようにしておきたいところです。
また1年生においては、都立入試では必須の「図形の作図」を習いますので、「角の二等分線」と「垂直二等分線」を軸として、入試を意識して練習していきましょう。
中学2年生時の対策
中学2年生のときも、1年生のときと同様に「全ての単元の問題に正解できる力」を身につけていきましょう。
難しい問題に正解することではなく、とにかく「教科書の節末問題」と同じレベルの問題に「ミスなく正解する力」を身につけたいところです。
中学2年生では、特に「一次関数」と「図形の証明問題」において、上記の力を必要とします。
特に「日比谷対策」に限って言えば、一次関数においては以下のような「変域の決定問題」が例年出題されていますので、繰り返し練習して下さい。
令和3年度の問題

令和4年度の問題

令和5年度の問題

中学2年生までの内容で「教科書の節末問題」と同じレベルの問題を理解できると、入試に必要な力をほぼ身につけられたと言っても過言ではないです。
中学3年生時の対策と勉強法
さて、中学3年生となると、1、2年生のときと比べて、もう少し細かく「入試対策」というものを見ていく必要があります。
というのも、都立入試である以上「内申点の確保」も大事になってくるからです。
東京都の都立入試は「中学3年生の2学期の成績」と「本番での入試得点」の総合得点で合否が決まります。
ですので、中学3年生においては「内申の確保」と「入試学力」の両立が大事になってきます。
この視点をもとに、まずは1、2学期にすべきことを、以下で解説します。
中3の1学期にすべきこと
今まで通り、3年生で習う基本的な内容は全てできるようにしておきましょう。
学校の定期テストでは、満点を狙って下さい。
定期テスト対策に並行して「典型的な入試問題」を勉強メニューに加えましょう。
具体的には、1、2年生の内容の「教科書の節末レベル問題」を再度復習することをおすすめします。
塾に行っている方は「新中学問題集」などの問題集に載っているような、いわゆる「標準問題」を勉強に取り入れると良いでしょう。
さらに余裕がある方は、中学3年生の内容を先取りすることも視野に入れて下さい。
というのも日比谷高校の数学は、6割以上「2、3年生の内容の融合問題」が出題されます。
先取り学習を希望の方は、当会の「高校受験対策フルサポートコース」でも対応可能ですので、ぜひ一度ご相談下さい。
中3の夏休みにすべきこと
夏休み期間中は、先取り学習を基本として、中学2年生までの内容を題材とした「典型的な入試問題」を「ミスなくできるようにする」ということを、学習の目標にしましょう。
夏休みの間は、学校の授業は進まない分、塾などで先取り学習ができるようにして「二次方程式」「二次関数」「相似」の基本までを習得できることが理想です。
「典型的な入試問題」と書きましたが、例えば関数の問題だと「座標平面上の三角形の面積を二等分する直線を求める問題」などに正解できると良いです。
三角形の合同証明の問題であれば、単に三角形の問題ではなく「二等辺三角形」「平行四辺形」の性質を使って解ける問題なども練習してみて下さい。
中3の2学期にすべきこと
中3の2学期は、内申点の確保と同時に「難関校で出題される典型的な入試問題」を勉強メニューに加えることが大事です。
例えば難関校の入試では、関数の問題であれば「二次関数」からの出題は、どうしても避けて通れません。
ですので、夏休み中に二次関数の基本を習得できた方は、まずは二次関数の典型問題の解き方を身に付けましょう。
同時に「相似の証明」「円の性質」「三平方の定理」など、難関校では必ず出題される単元の基礎を、遅くても12月に入るまでには習得しましょう。
本番で高得点を狙う勉強法
さて、ここまでお読みいただくと分かる通り、日比谷高校をはじめ難関校を受ける場合は、中3の2学期中に「中3の全範囲の基礎」を習得することが必須となります。
このことを前提として、本番で高得点を狙う勉強法について解説します。
中3の冬休みにすること
2学期の期末テストが終わったら、すぐに過去問に取りかかって下さい。
都立校の入試問題の場合、過去10年ほどさかのぼってみても、出題傾向はほとんど何も変わりません。
ですので、書店で過去問を購入したら、年度の新しい順でも古い順でも良いので、まずは1年分解いてみて下さい。
冬休み中は過去問演習に加えて、何度も言うようで申しわけないのですが「難関校で出題される典型的な入試問題」を練習して下さい。
おすすめ問題集
それでは、そうした「典型的な入試問題」が載っている問題集を紹介します。
まずは「体系数学」がおすすめです。
体系数学はもともと中高一貫校生に向けの参考書・問題集です。
しかし、載っている問題を見ていると「難関校で出題される問題を解くための考え方」を身に付けられる例題がたくさんあります。
数学が苦手な方は、まずはそうした例題から学ぶことをおすすめします。
次は、塾に通っている方はすでにお持ちかもしれませんが、新中学問題集がおすすめです。
全学年分揃える必要はなく、むしろ3年生用だけでも購入して問題演習できると良いでしょう。
受験直前期の勉強
入試直前期は過去問をメインに問題演習をしましょう。
おすすめは、東京学参の過去問題集です。
解けなかった問題があったとしても、解説を読んでからもう一度解き、さらにその問題と似た問題を何度も解くことで理解が深まります。
過去問を解いてみて、間違えた原因を探すことはもちろん、できた問題であっても「なにがきっかけで正解できたのか」「正解できた理由は何か」を見つけましょう。
そうすることで、「これを考えることなしに問題は解けない」と思えるような一つのきっかけに気付きます。
この時期は、苦手克服というよりは「できるようになったことが継続的に、今でもできるかどうか」を確かめ続ける期間です。
都立日比谷高校の数学 解答時間の配分と解答戦略

次は入試本番の時間配分と試験戦略について解説します。
このセクションを読むことで、適切な時間管理と、本番で高得点を取るための効果的な対策を理解できます。
解答時間配分のポイント
都立日比谷高校の数学の試験時間は50分です。
見直しの時間まで含めて問題を解く時間を考えると、時間配分の目安は以下の通りです:
- 大問1(小問集合):10分
- 大問2(二次関数):12分
- 大問3(円と図形):12分
- 大問4(空間図形):12分
しかし、これは全問解き切るための時間配分の一例です。
各個人の持つ得意不得意によっては、一問一問にかけられる時間は変わってくることもあり得ます。
例えば、「関数のグラフの問題は苦手で小問1だけ解ければよい」という生徒さんであれば、大問2は3~4分だけ使って大問3に20分使ってもよいでしょう。
このように、自分が最も点数が取れるように時間を使うことが重要です。
入試本番の解答戦略
試験戦略としては、「解ける問題を確実に解く」「解けない問題に時間をかけない」ことがポイントです。
過去問を実際に解いてみると分かる通り、各年度において、必ず「各大問の (1) 番の問題」は、教科書レベルの基本問題に帰着される問題が出題されます。
特に数学が苦手な方は、「小問と各大問の (1) 番の問題 」だけでも点数を取るようにしておくことができると良いですね。
「解けない問題」に時間を使ってしまったために、「解ける問題」を解く時間がなくなってしまったということは避けるべきです。
解けない問題に時間を使うより、解いた問題にミスがないかどうかを見直した方が、点数確保を望めます。
日比谷高校の数学の過去問に関するよくある質問

Q1: 自校作成問題とは何ですか?どういった特徴がありますか?
A1: 自校作成問題とは、学校独自で作成された問題のことを指します。
都立高校の入試問題は、マークシート方式で各教科の100点満点の試験で、どの高校でも同じ試験で合否判定を行います。
しかし、日比谷、国立、西、戸山、青山などの一部の「進学指導重点校」では国語・数学・英語の3科目については、各高校が独自に作成した問題を入試に使用します。
それが「自校作成問題」と呼ばれるものです。
大きな特徴としては、「中学3年の後期に習う内容」が出題範囲の中心となるため、難易度も高く対策も難しくなりがちです。
ただこの記事でも書いてきた通り「典型的な入試問題」を解く練習を繰り返すことで、本番で高得点を狙うことも可能です。
Q2: 日比谷高校の2023年度の数学の過去問はどういった傾向がありますか?
例年通り、どの大問においても「中学3年生の内容の融合問題」が出題されています。
図形の問題を解くとよく分かりますが、難しい問題を解くこと以前に「典型的な入試問題」に、自分で帰着させる力が大事です。
このことはつまり、日頃から「何をきっかけとして正解できたのか」を振り返る習慣を求められる問題が特に多いということです。
Q3: 他の高校(例:西高校、戸山高校)の過去問と日比谷高校の過去問との違いは何ですか?
ほとんどどの過去問と比べても、難易度と出題範囲に大きな違いはありません。
しかし、細かいところで、例えば図形の問題で「辺の比」を求める際に、「連比」を使う問題とそうでない問題があるなどの違いはあります。
特に日比谷高校の問題を見ていると、辺の比を求める際に「相似な三角形を自分で探す」というプロセスを求められる問題が多い印象です。
この他にも、2次関数の問題で「大問の (3) だけは、どうしても時間内に解くのは無理」と言わざるを得ない問題を出す高校もあります。
これに対して日比谷高校は、そうした「大問の (3) 」も、数学に自信のある受験生であれば解ける内容になっていることがほとんどです。
まとめ
この記事では、都立日比谷高校の数学の過去問についての傾向や入試対策を解説しました。
大事なポイントは、以下の通りです。
- 過去問の特徴と傾向: 日比谷高校の数学の問題は、典型的な入試問題の類題が多く出題されます。また、都立独自の出題形式も知っておくことが大事です。
- 解答例と解説: 各大問ごとの解答例を見てみると「相似な三角形を探す」というポイントが共通しています。この考え方は、辺の比を求める問題で重要です。
- 対策と勉強法: 中学1・2年生においては、教科書の基礎を特に大事にして下さい。難しい問題を解く練習は、3年生からでも十分間に合います。
- 時間配分と試験戦略: できる問題で確実に点数を取るようにしましょう。大問の1番で得点できることが大事です。
出題傾向と問題を解くための考え方を理解し、適切な対策を行うことで、入試において高い得点を目指すことができます。
この記事が、日比谷高校に挑むすべての受験生の役に立てれば幸いです。

【こんなお悩みありませんか】
・基本はできるけど、入試問題だとできない
・先取り学習したいけれど、進め方が分からない
・勉強しているけれど、いまいち偏差値が上がらない
・集団塾の補習をしたいが、良い個別指導が見つからない
・日比谷高校の数学対策は難しい
高校受験生に向けて、当会では単発の家庭教師指導の他、「高校受験対策フルサポートコース」もご用意しております。
随時無料相談、体験授業も行っておりますので、ご相談事がありましたら、、以下のフォームよりいつでもお問合わせ下さい。
