「ミス」ではなく「勘違いや思い込み・知識不足」

こんにちは。プロ家庭教師、数学学習コンサルタントの鈴木です。

今日はお子さんが、決して「ミス」をしているのではなく、「こんなことを勘違いしている場合があります」ということについて、お伝えしていきます。

前回、以下の記事で、ミスのタイプやその原因について書いてきましたが、それらはどれも、「頭の中では正しく考えることもできているのに、書くことや見るポイントを間違えて出てきた結果」のことです。

https://sugaku1bann.com/2021/10/28/kearesumisunoshoutai/

ここからは、そもそも「自分では今まで正しいと思ってきたことが、実は間違った形で覚えていた」ということが、浮き彫りになる例について書いていきます。

割り算のミスの例でも出てきましたが、「大人から見るとケアレスミスをしているように見えるけれど、子どもから見ると正しいことをしているつもり」になっていることが、中学受験算数や中学以降の数学では、割合として多くなってきます。

これから以下に書くようなことが、お子さんの中で分かっているのにもかかわらず、問題の答が間違っていたとします。

そのときに、お子さん自身が「何がいけなかったのか」ということに、気が付けるのであれば、それは「ミス」であり、どんな見直し方をすればそのミスが防げるのかといった解決策を考えていくことができます。

しかし、以下に書くようなことにおいて、そもそも知らないであるとか、勘違いしたままインプットしているということがあれば、それはミスではなく、「知識不足」や「勘違い」「思い込み」ということになります。

問題文の読み方を知らない・または勘違いしている

算数にも数学にも共通して、「問題文の読み方」というものが存在します。

ときどき指導の中で、生徒さんに問題文を読んでもらって、「この数は問題文の中にある何の量のこと？」と聞いてみたときに、全く違うものが答として返ってきてしまう場面もあります。

その原因の一つに、問題を作った人が「どの数がどの言葉とつながっているのか？」ということを、解答する人に意識させるような、「算数や数学独特の問題文の表現やその読み方」を,、お子さんが知らないことがあります。

読み間違いが多い典型問題

一つ例を挙げます。

例題　１本８０円のえんぴつ５本買えるお金で、おなじ金額のボールペンを４本買いました。ボールペン１本の金額はいくらですか。

上の例題ではまず、「１本８０円のえんぴつを５本買えるお金」を「４００円」に言い換える必要があります。

この「言い換える操作」が算数や数学ではよく出てくるのですが、お子さんによっては、上に書いたような問題において、「そんな読み方をすることを知らない」と思っている場合があります。

上の問題文は逆に「とある人がお金を持っていて、そのお金で１本８０円のえんぴつを５本買えるんだって！」という風にも言い換えられると、問題を解くヒントが得られますが、ここでもやはり「言い換え」は必須です。

お子さんが特に、文章問題を解く際に分からないと感じているのは、一つには「問題文の言い換え方」を知らないことに由来する場合も多いのです。

読み方を勘違いしている具体例

また上の問題文では「おなじ金額」いう言葉が出てきますが、この言葉が「何と同じなのか」という意味を、勘違いしている場合もあります。

具体的には、「えんぴつとおなじ金額」と勘違いしている場合があります。

この場合、「何かとおなじ金額のボールペン」というわけではなく「ボールペンが全部おなじ金額」であることを意味するのですが、ここでも「そう読むことを知らない」可能性が出てきます。

お子さんがこの問題を解答して、仮に✖がついたとき、それは単に計算ミスやケアレスミスなどではなく、「問題文の読み方を知らない」ことが原因で正解できていない可能性があります。

計算のルールを知らない

算数にも数学にも共通して、計算のルールというものがあります。

高校の数学だと特に、「定義」という言葉が出てきて、その定義の通りに計算する場面がありますが、その定義を知らない高校生も多いです。

四則計算の例が典型的ですが、四則計算は、計算のルールに沿って計算しなければいけない例の一つです。

お子さんが、四則計算のルールを知らないという実例については、以下の記事でも解説しております。

https://sugaku1bann.com/2021/10/26/misudewanakuseikaisitatumori/

中学数学で多い「計算の仕方を知らない例」

他にも中学の数学で、「正負の数」の計算問題を解く場面において、お子さんが計算の仕方やそのルールを知らないことが、明らかになるときもあります。

よくあるのが、「５－(－３)」といったタイプの計算問題で、答が「２」などとなっていることです。

符号の見落としなども考えられますが、その場合は「見落としが原因のミス」であり、「式全体をもう一度見返すこと」などが、ミスを防ぐ対策の一つです。

ところが、「マイナスの数を引く」ということが、結果足し算になることを知らなかったのであれば、それは「知識不足」ということになります。

知識不足解消のための小アドバイス

こうした知識不足が明らかになった場合には、「５－(－３)」の計算方法を学んだあとに「6－(－１)」などの計算問題を解き「同じ見方・考え方で解ける問題を繰り返し解く」ことで、知識不足からは抜け出せます。

あとでも述べますが、知識不足や勘違いのせいで、違った答を書いてしまうお子さんは「同じ考え方で解ける問題を何回も解く経験」が少ないです。

色んな問題を解くことよりも、まずは「同じ考え方で解ける問題」を、何回も解くという経験が大切です。

「平行」や「垂直」だと思い込んでいる

思い込みが原因で、お子さんとしては正解を出したつもりなのに、答が違っているということがよくあります。

また、思い込みがあるせいで、答が合っていたとしても、たまたま答が合っているということもしばしばあります。

そうしたことが起きてしまう原因を説明する具体例が、与えられた図形を見て「こことここは平行になっている」「この線とこの線は垂直に交わっている」と決めつけてしまっていることです。

平行になっている、あるいは垂直になっているというのであれば、それがいかにして分かるのかを、本来であれば理由をもって説明できなければいけないのですが、思い込みが先行してしまうタイプのお子さんだと、「何となくそう思ったから」という説明の仕方になってしまうことがあります。

この例からから分かることは、「自分が考えていることが正しいかどうか」ということを、どんな方法で、どのタイミングで確かめるのかを、お子さんはそもそも知らない場合があるということです。

つまり、「何をすることが見直しすることなのか」を、お子さんは知らない場合があるのです。

問題文を振り返ることで思い込みがなくなる一例

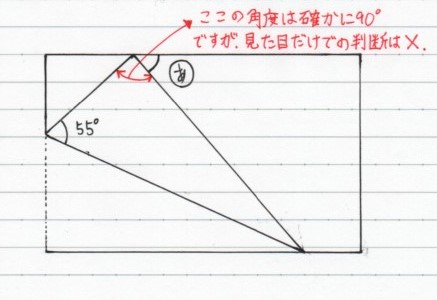
私が見てきたお子さんの中にも、図形の角度に関する問題を解いてもらったときに、答は合っていたものの、どう解いたのかを説明してもらう場面において、「ここは本当に90°になる？」と私から聞いてみたときに、「分からない」と答えた人がいました。

例えば、上に載せたような、長方形の一部を折り返すテーマの問題で、同じ角度を探しながら、角度を求めていくプロセスにおいて、その生徒さんは、図中の赤い部分の角度が「なんとなく90°に見える」という感覚に任せて、赤い部分の角度が90°となることを、明確な理由を持たずに認めてしまうということもありました。

上に載せた問題においては、問題文に書いてある条件 (つまり長方形を折り返したという一文) を振り返れば、赤い部分の角度が90°になることは、「折り返した三角形を、折り返す前の状態に戻せば、赤い部分はもとの長方形の一区画と一致する」という明確な理由を持って、説明することができます。

そのお子さんは、赤い部分の角度が90°になると思い込んでいたのですが、問題文をもう一度読み、与えられた図の中に、お互いに一致する角度はどこになるのかを、印なども描き込んで確かめることで、改めて赤い部分が90°となることに、納得できました。

さらにお話を聴くと、その生徒さんは他の図形に関する問題を解く際にも、問題文を一度読むだけで、与えられた図形の中に、問題文に書いてあるどの条件が反映されているのかを、振り返ることや確かめることをせず、見た目に任せて解こうとするときがあることも分かりました。

この例のように、図形を折り返す問題では、「折り返す前の状態を考えて、図中のどの部分とどの部分が一致するのかを確かめること」で、具体的に角度を求めるきっかけが生まれ、それをすること自体が見直しをすることにもつながります。

問題文を振り返ることに加え、「何をすることが見直しなのか」「なぜそれをすると見直しができたことになるのか」ということについて、明確な答を持つことが大切です。

その他思い込み

「平行」や「垂直」に限らず、思い込みの意識を持ったまま問題を解いていることが分かる場面は多く、図形分野においては主に、他にも以下に書くようなことを、思い込んでいる場合があります。

・「辺」を答えなさいというところを「面」を答える

・「表面積」を答えるところを「体積」を答える

・「円周の長さ」を答えるところを「円の面積」を答える

・与えられた直角三角形を、辺の比が「3:4:5」だと思い込んでいる

・与えられた直角三角形を、「30°、60°、90°」の直角三角形と思い込んでいる

・立体図形の切り口を、本来できる図形とは別の形だと思い込んでいる

・問題で与えられた図に追加で線を描き込み、できた三角形を正三角形だと思い込んでいる

・自分が描いた図を見て、正しい位置関係で描けていると思い込んでいる

「正しい位置関係で描けている」と思い込んでしまっているというのは、具体的にいうと「２本の線分ｌ、ｍがあって、本当はｌの方が長いのに、ｍの方を長く描いて、そのまま問題を解こうとする場面」などがあることで、分かるケースが多いです。

そうしたとき、私からお子さんに対して「その図は正しい？」と聞き、「ｌの方が長いんだった」という返事が返ってきて、「ｍの方が長いと思ってた」などと言われると、それは間違いなく思い込みによる「ミス」が起きていると分かります。

ところが、例えば直角三角形の辺の比を「3:4:5」だと思い込んでいるお子さんがいたのですが、よく話を聴いてみると、そのお子さんは「直角三角形はどれも辺の比が3:4:5」だと思っていたそうです。

この実例は、「自分の考えが間違っているということを知らないケース」があることを示す一つの例です。

この場合は「ミス」ではなく、間違いそのものを正しいと思い込んでいた結果として、誤答を出してしまっていることになるので、思い込みをなくせるような具体例を知ることからやらなければいけません。

ここまでお伝えしてきたことを、動画でも解説しておりますので、ぜひご覧下さい。

https://youtu.be/XBQHLzgqrjE

図形の種類を知らない・または勘違いしている

図形と一言で言っても、与えられた図形には一つ一つ名前がついており、それぞれ「どんな決まりのもとに、名前がついているのか」が決まっています。

これから述べることは、特に図形の面積を求める問題において、与えられた図形を見て「思い込み」や「勘違い」が原因で、どんな図形なのかを正確に判断できない結果、答が間違ってしまう例です。

問題で与えられた図形が、「どんな名前がついていたものなのか」を正確に判断できないということは、「こういった特徴をもつ図形を〇〇形と呼ぶ」といった、一つの決まり事を知らない可能性があります。

仮にその決まり事を知っていても、どんな図形になるのかの「見分け方」を知らずに、問題の答が違っていたとしたら、それは「図形の見分け方を知らないことで、答が間違っている可能性が高い」ということになります。

いずれにしても、これらのことが原因で問題の答が違っていたとしたら、それもやはり「知識不足」となっている部分や「勘違いしている部分」がお子さんの中にはあります。

安易に「ケアレスミス」とは言えません。

図形の名前を「聞いたことがあるだけ」になっている実例

例えば、「台形ってどんな形？」とお子さんに聞いたときに、すぐに答えられるのであれば、「いびつな四角形」の面積を求める問題も、正解することは難しくはないはずです。

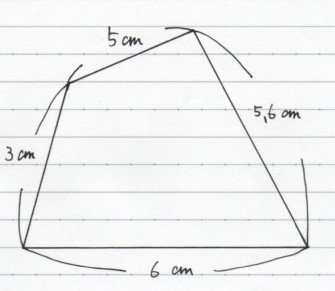
ここでいう「いびつな四角形」とは、以下に描くような、「四つの辺の長さがお互いに違うような四角形」を指すとします。

この四角形を見ると、四つの辺の長さが分かっていますよね。

このときに、「台形とはどんな形のことを言うのか？」が分かっているお子さんは、上の図を見て面積を求める際に「(５＋６)×３÷２」などという式を立てることは、可能性としては低いと言えます。

ところが、台形という言葉、その面積を求める公式を聞いたことがあっても、「台形とはどんな形なのか」を正確に言えないお子さんが、上に書いたような式を立てて答を出そうとしていたことがありました。

もっと言うとそのお子さんは、「底辺とは何か？高さとは何か？」が理解できていませんでした。

これは実際にあった、台形とは何かを知らないのに、「台形の面積を求める公式だけは言える」という実例です。

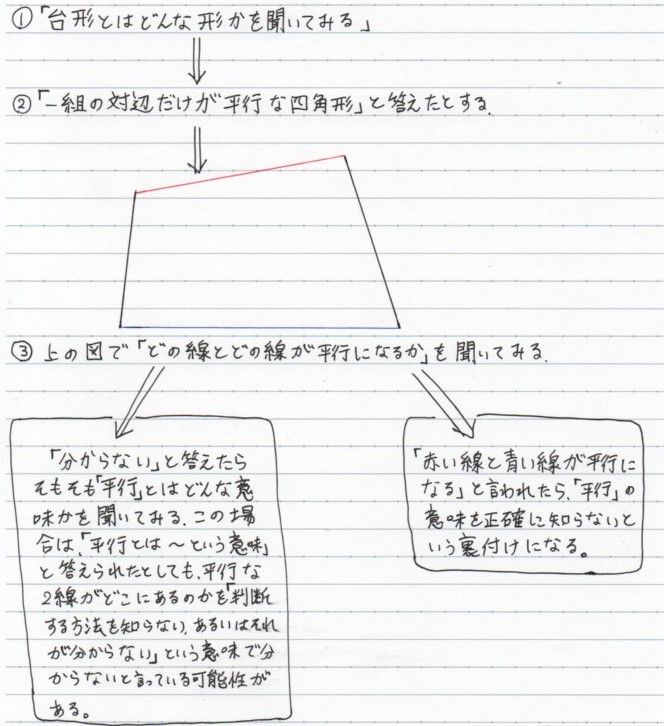
台形とは「一組の対辺 (だけ) が平行な四角形」のことです。

上に描いたような図形を見て、「(５＋６)×３÷２」といった式を書いてしまったときに、お子さんに「どうしてその式が出てきたのか？」を聞いてみて、「台形だから」と答えたとします。

そのときに、「じゃあ台形ってどんな形？」ともう一度聞いて、正確に答えられなかったのだとしたら、そもそも「台形そのもの」を正確に知らないことが原因で、答が違っています。

図形の「見分け方」を知らないこともある

「台形がどんな形か」を答えることができているのに、上の図形を見て「なぜ台形にならないのかが分からない」のであれば、その原因は以下で述べる２つの原因が考えられます。

まず一つ目は、「お互いに平行な１組の対辺」を見つけるために、図形中にあるどこの何を見れば良いのかを知らないということです。

つまり、「台形の見分け方」を知らないのです。

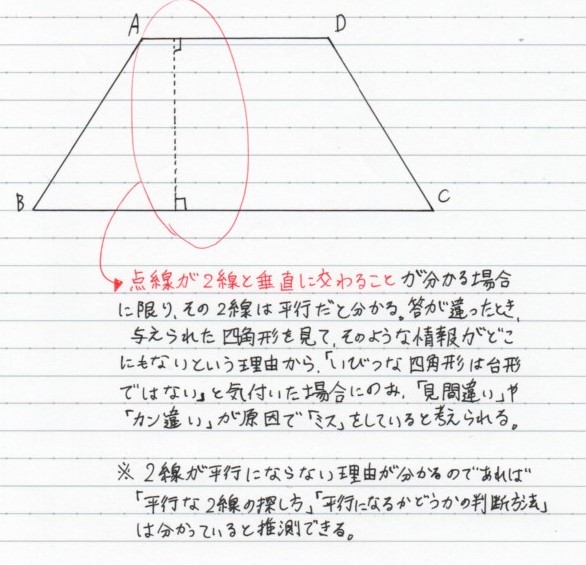
具体的には、四角形の一辺の上にある点から、お向かいの辺の一点まで点線が伸びていて、その点線がどちらの辺とも90°で交わるということが、印などもつけてあることによって分かる場合に限り、１組の対辺が平行だと分かりますが、そうした点線や印を見つけることで、平行な二線を探せるということを知らないのです。

逆に、そのような判断の仕方があることを知っていれば、上に描いた「いびつな四角形」を見て、「どことどこが平行になるなんて、どこにも書いていない！」と自信を持って答えられるはずです。

ですので、この場合は、「なぜ台形にならないのかが分からない」という気持ちに加えて、「台形になるのかならないのかがよく分からない」という気持ちも、お子さんにはありそうです。

こうした、お子さんが「台形かどうかを判定できない」という例は、これも実際に私の指導経験の中でありました。

以下、こんな会話を当時の生徒さんとしてきたことで、お子さんによっては、台形の見分け方を知らない場合もあることが分かりました。

生徒「先生、これ台形になるの？」

私「これ？そもそも台形ってどういう形だっけ？」

生徒「一つのところだけ平行になっているやつ？」

私「うん、そう。だから例えば、もしこの辺とこの辺が平行だったら、この図の中にそれが分かるヒントが描いてあるんだけどな・・・」

生徒「え、何が描いてあるの？」

私「この辺とこの辺の間に点線が描いてあって、その点線がこの二本の線とどう交わっていたら、この二本の線は平行になる？」

生徒「あー、90°になってれば良いってこと？」

私「そうそう、ちなみに、どうしてこの点線が90°で交わっていたら、平行になってるって言えるのかな？」

生徒「どこに点線を描いても、90°で交わっているから、この二本の線はぶつからないから？」

私「そうなんだよね。今までこういう四角形を見て、どことどこが平行になっているかとか、どうやって調べてた？」

生徒「え、問題を解くときに、そんなこと調べるなんて知らなかったんですけど・・・。」

私「そうかー、じゃあこういう点線をたよりに平行かどうかを考える方法は・・・？」

生徒「それ初めて知った！」

図形の特徴を勘違いしている可能性もある

「なぜ台形にならないのかが分からない」という様子がお子さんにあったとして、考えられる二つ目の原因は、お子さんが口頭によって言葉で「台形とは何か」を答えることができても、図を描いて説明してもらったとき、口頭で答えたことと図に描いたこととが、一致しない場合があるということです。

つまり、どんな図形を表すのかを「勘違い」していることが分かる場合です。

この場合は、「なぜ台形にならないのかが分からない」というよりはむしろ、「台形ではないと言われることに納得がいかない」と言った方が正しいかもしれません。

そのときは、そもそも「平行」の意味を知っているかどうかを、図に描いて説明してもらうことで、図形の種類のみならず、その図形を説明する際に使う言葉も、知っているかどうかを確かめることが必要です。

また一方で、「四角形の向かい合う２辺は、必ず平行になっている」などと思い込んでいる部分がないかどうかも、確かめる必要があります。

上で述べた例は、図形の「見分け方」を知らないことや、どんな図形かを「勘違い」していることに由来する間違いの一つで、決して「ケアレスミス」などとは言えない一例です。

後でもう一度図形を見返して、お子さんが「対辺が平行になることが、どこにも書いていない！」ということに気づいた場合に限り、思い込みなどが原因で「ミス」が起きていると考えられます。

面積を求める問題であればなおさら、図形を見て面積の式を立てる前に、「本当に〇〇形かな？ここを見て、これがこうなっているから、〇〇形と言える」という具合に、与えられた図形をもう一度見て、自分が考えたことが、図形の決まり事と一致しているかどうかを振り返ることが、ミスを防ぐ対策の一つとなります。

また、図形がどういった形になっているのかについて、過去にどう見極めてきたのかを思い出すことも大切です。

ここまでお伝えしてきたことを、動画でも解説しておりますので、ぜひご覧下さい。

https://youtu.be/RrjYACfsQ1o

立体の捉え方や体積の求め方を勘違いしている

与えられた図形が「どんなきまりのもとに、どういった名前がついていたのか」を知らないがために、その図形の種類を正確に判断できないことが原因で、問題を解けない (あるいは解いたとしても答が違い、何がいけなかったのか分からない) ということが、立体図形の問題を解く場合にもあり得るというお話です。

算数でよくあるのが、「柱体」と「錐体」が、それぞれどういった特徴を持つ立体なのかを、理解できていないということです。

このことは、例えば「台形柱」など、「どこを底面とすると柱体と捉えられるのか」が問われるような問題を解いてもらうと、「柱体」とはどういうものなのかを理解できているかどうかが分かります。

下の図のような台形柱において、台形を底面とせずに、側面である長方形が底面となっているとします。

この図をお子さんに見てもらい、そもそもどういう名前が付く立体図形なのかを聞いてみると、「柱体」に対する理解がどの程度のものなのかが分かります。

もし「台形柱」とすぐに答えられるのであれば、どうやって体積を求めるのかを説明してもらうことで、「柱体をどう捉えると体積が求められるのか」が理解できているかどうかを、把握することができます。

柱体であることの確かめ方

ところが「台形柱」とすぐに答えられない場合、問題を解く際に、以下に述べるような考え方を使うことを、そもそも知らない可能性があります。

１．与えられた立体図形を、図にある位置関係のまま捉えるのではなく、別の面を底面と考えて、立ててみたところを考えること

２．底面に平行な面で立体を切ることを考えたときに、「どこで切っても同じ形が現れるのはどんなときなのか」を考えること

「１．」の場合は、例えば親御さんや先生がお子さんに、「この面を下にすると、どんな立体になることが分かる？」と聞いてみて、「台形柱になっている」と答えられるのであれば、それは台形柱を知らないのではなく、「与えられた立体図形が、実はどんな形をしているのかを把握するために、図形を多方面から見ること」を知らない、または忘れているということになります。

「２．」をもし、そもそも知らないというのであれば、お子さんが仮に「別の立体図形の名前」を答えた場合、「〇〇柱であることをどう判断するのか？」を知らないか、あるいは「柱体とはどういうものなのか」を知らない可能性があります。

図形全般に言えることですが、形にはそれぞれ名前がついていること、名前が付く際には、かならず「決まりごと」がもとになっていることを思い出すことが大切です。

こうしたことは、数学を学んでいくにあたり、いわゆる「定義」として与えられたものを、自分勝手な解釈ではなく、具体的な「数学の中で出てくるもの (数や図形) 」と結び付けて受け入れることにつながります。

お子さんが立体図形の体積の問題を解き、答が違っていたとしたら、それは単に「計算ミス」ではなくて、問題の中で与えられた図形の捉え方そのものを勘違いしていることが原因で、答が違っていることもあり得ます。

ここまでお伝えしてきたことを、動画でも解説しております。

こちらが動画のリンクですので、ご興味ある方はぜひご覧下さい。

https://youtu.be/YiPiB0yRv6k

数学用語を正しく覚えていない

中学の数学からは、一つの計算問題を解くにしても、言葉を意識して解かなければならない場面がよく出てきます。

そういった場面に遭遇する最たる例は、中学２年で出てくる「変化の割合」を求めることです。

数学用語を知らないことが明らかになる典型事例 (変化の割合)

変化の割合とは、例えばｘとｙとの間に「ｙ＝－２ｘ＋６」という関係があったときに、「ｘの値が－１から３まで変化したとき、ｘの値が増加した量と、ｙの値が増加した量との割合」のことを言います。

しかし、この「変化の割合」という言葉の意味を、お子さんが正しく把握できていないことがあります。

というのも、よくある勘違いが「ｘ＝－１のときｙ＝８、ｘ＝３のときｙ＝０だから、ｙの値が増加した量は８」としてしまうことです。

「増加した量」という言葉から、「大きい数から小さい数を引く」ものだと思っていたという声が多いのですが、それは完全な「勘違い」であり、「数学で使われる言葉を正しく覚えていない」ということが起きている具体例の一つです。

もし、「ｘ＝３のときの値から、ｘ＝－１のときの値を引いて、ｙの値の増加量が出ること」を知っているのに、書き間違いなどが原因で答が違っているのであれば、それは「ミス」であり、「どんな行動をとればミスを防げたのか」を考えることができます。

しかし、そもそも「変化の割合」「増加量」という言葉が、数学の言葉として何を意味するのかを知らないまま問題を解いていたとしたら、それはミスではなく知識不足ということになります。

「ケアレスミス」というものではありません。

数学記号の意味を覚えていない

中学の数学では、高校の数学ほど多くの記号が出てくるわけではないのですが、「その記号には、そんな意味が込められていたんだ・・・」と、あとから自分の勉強不足に気づくお子さんも多いです。

高校の数学ともなれば、それこそ「サイン・コサイン」や「ログやシグマ」に代表されるように、一つ一つの記号が何のことを言っているのか、そもそも正しく知らないことが原因で、ミスしているのではなく、「勘違い」によって正解できていない場面がよくあります。

数学記号を覚えていない典型事例 (平方根)

記号の意味を正しく覚えることが求められるのは、中学３年生で習う「平方根」の単元が最初ではないかと思います。

もちろん、中学１年生の平面図形では「平行」「垂直」を表す記号や、中学２年生で習う三角形の合同で出てくる記号なども出てきますが、平方根の記号「√」の意味を、100%正確な意味で覚えているかどうかは、指導の中でその都度確かめていくことの一つだと感じています。

というのも、まずは例えば「４の平方根」を例に、お話をしていきます。

「４の平方根」とは「２回かけて４になる数のこと」です。

「√４」とは「２回かけて４になる数のうち、プラスの方」という意味を持つ数のことです。

これらのことから・・・

「４の平方根は何か」と問われたら、「＋２と－２」と答えるのが正解です。

一方で、「√４はいくつか」という問に対しては「２」と答えるのが正解です。

しかし、「平方根という言葉」＝「√の記号」などと勘違いしているお子さんは、上の問題を正解したつもりでも、テストの解答には✖がついていることがあります。

つまり、「４の平方根」を求める問題で、お子さんによっては「＋２」しか答を書いていなかったり、「√４＝＋２と－２」と答えてしまっている場合があります。

こうした解答をしてしまうのは、まさに、ケアレスミスなどではなく、「そもそも言葉の意味、記号の意味を正しい形で覚えていないことによる勘違い」であると言えます。

４の平方根を求める問題で、平方根の意味を知っているのに、マイナスの符号を「書き忘れた」ということであれば、それはミスであり、自分の書いたことを振り返ることなどが、ミスを防ぐ方法の一つとして考えられます。

私が見ている生徒さんも、「平方根を求めよ」という問題を解いてはじめて、「平方根の意味」を知ったということがありました。

何をもって「正解」かを知らない

中学以降の数学では、「どうすることが正解なのか？」を正確に把握しておく必要があります。

因数分解を例としてお話をしていくと、例えば因数分解を習いたての生徒さんに、「因数分解するって、何をすること？」と聞くと、正確に答えられない場面がしばしばあります。

因数分解するとは、ｘ＾２−３ｘ+２などという式を (x−１)(x−２) といった、いわゆる「カッコ×カッコ」の形や「数×カッコ」の形に、式を変形することなのですが、生徒さんの書いた答案を見てみて、全く式がその形になっていないものがあったときなどに、まさにそうした場面があります。

ここでもやはり、「計算ミス」や「ケアレスミス」などではなく、「因数分解しなさい」と言われたら、式としてどう答えることが正解なのかを、生徒さんはそもそも知らない (または覚えていない) という状況に置かれていることもあります。

「何をもって正解かを知らない」というのは、因数分解の例からも分かるように、計算プロセスや一つの計算結果を得ることに対しては、「それぞれ名前が付いていること」を知らないというようにも言い換えられます。

もっと例を挙げると、因数分解することの他にも、「文字式を計算すること」「式を展開すること」や「方程式を解くこと」「不等式を解くこと」とは、具体的に何をすることなのかを、お子さんは知らない場合があるということです。

方程式を解くというのは、「文字ｘを含む等式に当てはまるｘの値を求めること」ですが、こうしたことを知らないと、ｘの値を求めずに、文字式のみ式変形したものをテストの答案に書いてしまうような場面も出てきます。

「〇〇を答えなさい」と言われているのに、違うものを答えてしまうタイプのお子さんは、そもそも上に書いたような実例から、「何を答えることが正解か」を知らない、または勘違いしたまま知ったつもりになっていることがありそうです。

ここまでお伝えしてきたことを、動画でも解説しておりますので、ご興味ある方は、以下のリンクをクリックしていただき、動画もご覧下さい。

https://youtu.be/cVHwdhB1msw

まとめ (勉強法の小アドバイス)

この記事では、お子さんが具体的に、どういった場面において、何をどんな風に勘違いしているのかであるとか、何を原因として知識不足になってしまっているのかということについて、お話してきました。

勘違いや知識不足をなくすために、どんな意識を持って勉強していけば良いのかについて、まとめて書いていきます。

以下の記事でも詳しく解説しておりますので、ぜひご一読下さい。

https://sugaku1bann.com/2021/12/14/kihonnnominitukekata/

正解できたときのことを思い出す

勘違いをなくすために大事なのは、「どう考えれば正解できたのか」を思い出すことです。

例えば、問題文の読み方を勘違いしないように、問題文を読む際には、「以前こんな文章があったときに、こんな読み方をして正解がもらえたかどうか」を思い出すことで、勘違いしたまま文章を読み進めることを防げます。

図形がどんな形をしているのかを判断するときも同様で、「こんな風に判断することで、正解に結びついたかどうか」を思い出すことで、思い込みのせいで答が違うという状況をなくすきっかけにもなります。

基本例題で考え方を学ぶ

知識不足というのは、「勉強不足」であるとか、そもそも「勉強したことになっていない」と言った方が正しいこともあります。

算数、数学の勉強において必ずするべきことは、基本的な例題を解くことを通して、問題を解く際に使う「考え方」を学ぶということです。

ここでお話してきた、柱体の体積を求める問題を例にとれば、どの問題集にも載っているような立体の体積を求める問題をただ解くだけでなく、そうした問題を題材として、「柱体の判定方法」であるとか「底面積×高さ＝体積」といった、どんな問題を解く際にも必要になる知識を身に付けることが大事です。

考え方をマネして使う

上で説明した「考え方」を、他の問題を解くときにマネして使うことが大事です。

「この問題にはこの解き方」という認識ではなくて、「この問題もあの問題も、共通してこれを求めなさいという指示があるから、あのとき学んだあの考え方を使って解ける」という認識を持つことで、知識の定着を図れます。

そのためにも、色んな問題を解くことよりも、「同じ考え方で解ける問題を繰り返し練習すること」を、強くおすすめします。

正誤判断する

「ここではこの問題文を、こんな風に解釈して良いのか」であるとか、「ここでこんな図を描くことは、そもそも正しいことなのか」といった疑問を持ち、その疑問に一つ一つ答えていくことが大事です。

いわゆる自問自答することを通して、正誤判断をするということです。

そうしたプロセスを踏むことを身に付けることで、正解できたときのことを思い出すという意識にもつながります。

小学生にはまだ難しいのではという声もありそうですが、中学受験の算数では、そこまでの思考プロセスを経ないと、正解が出せないものも多いです。

難しい問題に手をつける前に、まずはここに書いたような「勉強を進めていく上で大事な視点」を身に付ける方が先です。

解答や解説を見ずに正解する

問題を解いて丸を付けて、✖になったものはそのままにせず、解説など何も見ずに正解できて、はじめて「勉強した」と言えます。

結局のところ「解説を読んだだけで、そのあと自分の力だけで正解できるまで問題演習できていない」ということが、知識不足に陥ってしまう最大の原因です。

解説など何も見ずに、基本例題を通して学んだ考え方をマネして使うことで、間違いなく正解が出せるという状態を作ることが、勉強をするという意味にふさわしいと言えます。