こんにちは。算数・数学専門家庭教師の鈴木です。
今回は題名の通り鷗友学園女子中学の算数の入試問題を解説します。
大問2の文章問題について解説し、大事な考え方をその都度お伝えしていきますね。
↓問題がこちらです↓

「なくなります」に注意!
この問題を見たとき「仕事算だなぁ」と思う人も多いのではないでしょうか。
仕事算というと「同じ量の仕事」を何人かでするというタイプの問題が多いですよね。
ですので私はこの問題を見たとき、ちょうど12日でイラストが「なくなる」にしても、3日で「なくなる」にしても「全部あわせてたら同じ枚数だった」と思っていました。
ところが図を描いてみると「1日でこんなにかけるのか?」と思うような枚数になってしまうことから「なくなるというのはもっと別の意味だ」と気づきます。
「全部の枚数」はトータルで違う

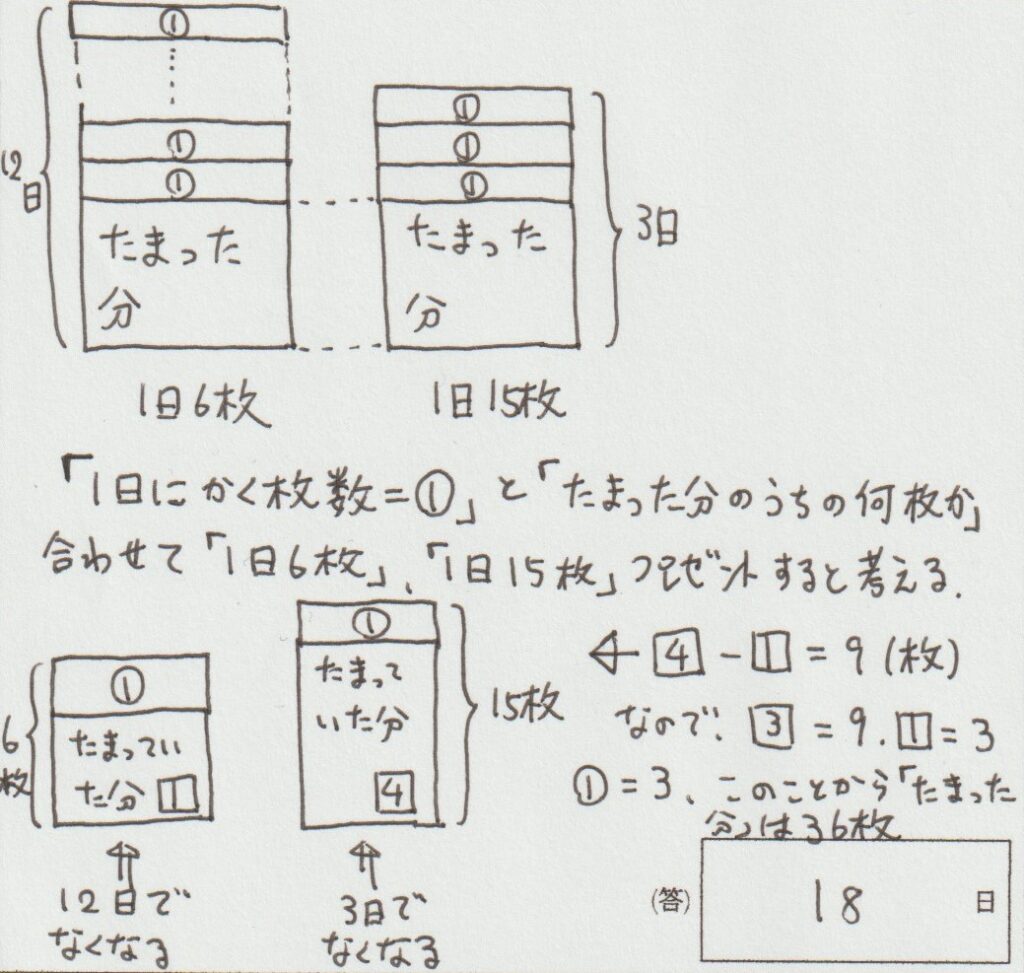
上に描いた図のように「もともとたまった分と12日間でかいた分を合わせた枚数」と、「もともとたまった分と3日間でかいた分を合わせた枚数」は、違って良いのです。
それらをそれぞれ「1日6枚ずつ」、「1日15枚ずつ」プレゼントしたら「自分のもとからかいたイラストがなくなった」ということなのです!
1日にかく枚数を①とおく
1日にかく枚数を①とおいてみますね。
するともともと「たまった分」がありますので、「①」と「たまった分のうちの何枚か」を合わせて「1日6枚」「1日15枚」プレゼントすると考えることができます。
「たまった分」は変わらない!
中学受験の算数では、食塩水の問題も特にそうですが「変わらない量を見つけること」が大事です。
この問題ではもともとかいたイラストの「たまった分」がありますよね。
この「たまった分」は「12日でなくなろうと、3日でなくなろうと、たまっていた分のトータルは変わらない」ということに気付きます。
たまった分を比の値で出す!
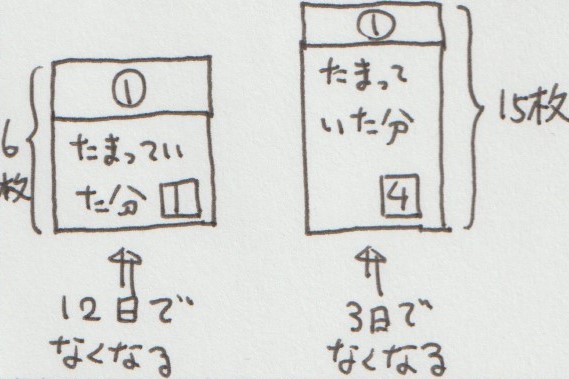
1日6枚ずつプレゼントするときの「たまった分から渡す枚数」を1⃣とします。
すると、12日で「たまった分」はなくなるので、たまった分全体は「❏の12」となります。
1日15枚ずつプレゼントすると、3日で「たまった分」はなくなるので、「4⃣」が「1日15枚ずつプレゼントするときのたまった分から渡す枚数」となります。
4⃣と1⃣の差を出し「たまった分全体の枚数」を出す
1日6枚渡しても、1日15枚渡しても「1日にかく枚数は同じ」なので、「たまった分から渡す枚数の差」は必ず9枚です。
こうした考え方は、中学受験の算数では大事ですよね。
このことから3⃣=9 (枚) となり、1⃣=3 (枚) となります。
ですので「たまった分全体」=「❏の12」=3×12=36 (枚) となります。
「1日にかく枚数」も分かるとこの問題の正解を出せる!
1⃣とは、1日6枚ずつプレゼントするときの「たまった分から渡す枚数」でしたね。
それが「3枚」でしたので、1日にかく枚数は「3枚」と分かります。
問題では「5枚ずつプレゼントしたら、何日でイラストがなくなるか」を聞かれていましたよね。
1日にかく枚数が「3枚」なので、5枚ずつプレゼントするときは「たまった分から2枚ずつ渡す」ことになります。
たまった分全体は「36枚」でしたので、2枚ずつ渡すとなれば「36÷2」で18日かかることが分かりますね!
勉強法アドバイス
最後に、私が実際に解答用紙に記入して解いたものを載せておきますね。
このような問題をできるようになるためには「基本的な問題から考え方を学ぶこと」が一番大事です。
特にこの問題だと、そもそも「問題文の読み方に気をつけること」が大事でした。
鴎友学園の問題を見ていると「問題文を読み、いかに基本的な問題に直せるか」が重要ですし、「比の考え方を使うこと」もよく出ます。
この問題は「比」「仕事算」「速さ」などの基本問題が混ざった問題と見ることができます。
問題を解くときに「どう考えれば正解できたのか」を振り返ってみることで、基本的な考え方を身につけられますので、ぜひ実践してみて下さいね!
↓中学受験対策フルサポートコース – 算数・数学オンライン個別指導塾 等々力・自由が丘プロ家庭教師 (sugaku1bann.com)↓