こんにちは。算数・数学専門家庭教師の鈴木です。
今回は題名の通り鷗友学園女子中学の算数の入試問題を解説します。
大問4の文章問題について解説し、大事な考え方をその都度お伝えしていきますね。
↓問題がこちらです↓
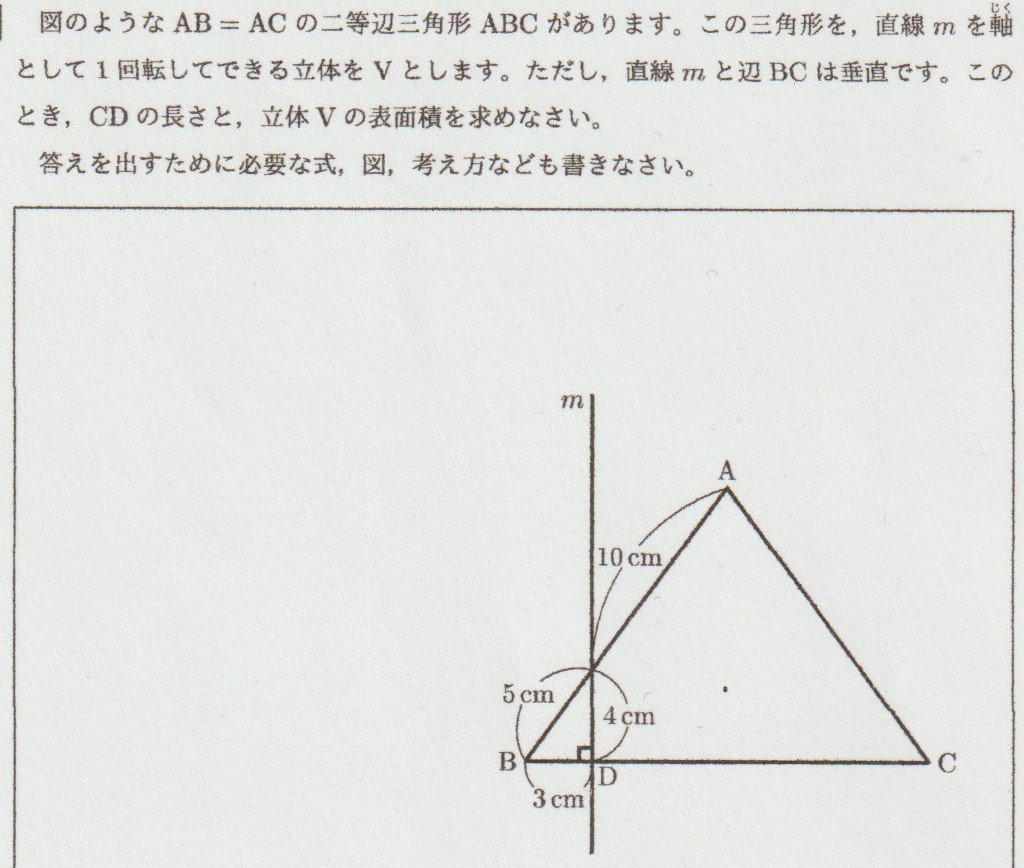
でき上がった立体図形を描く
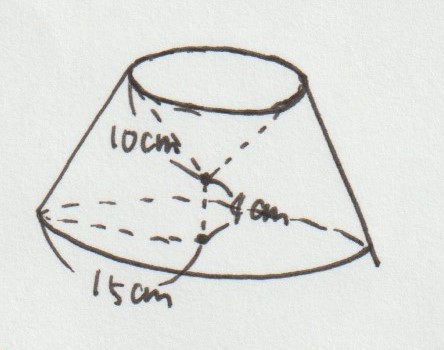
回転体の体積や表面積を求める問題の場合、必ず「でき上がった立体の形」を描くことが大事です。
実際にできた立体図形を描くことで「どこの長さがいくつなのか?」「どんな形であることが分かるのか?」も分かります。
ここでは上の図のように「円錐のとがった部分を取り、さらにくぼみを加えたような立体」ができます。
三角形の相似や合同に注目してCDの長さを求める
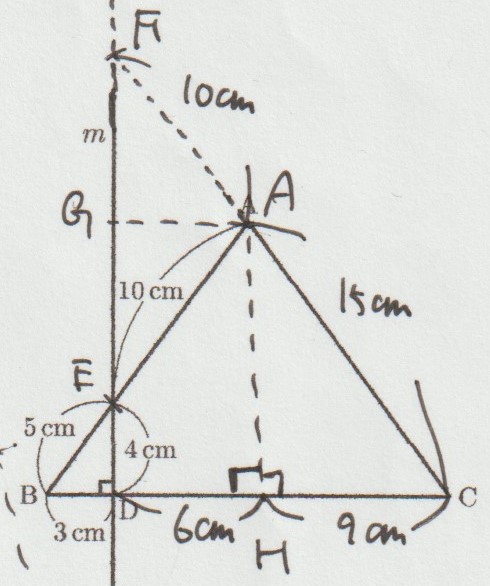
三角形ABHと三角形EBDの相似に注目する
上の図で、点Aから点Hまで書き入れることにします。
このとき、角AHB=90°となるように点Hをとります。
すると三角形ABHと三角形EBDが相似になっていますよね。
BE:EA=5:10=1:2 となっていますので、BD:DH=1:2 となることから、DH=6㎝になります。
三角形ABHと三角形ACHの合同に注目する
三角形ABCは「AB=AC」の二等辺三角形であること、三角形ABHと三角形ACHはともに直角三角形であることから、これら二つの三角形はお互いに合同になります。
ですので、BH=CH=9㎝となります。
というわけで、CD=DH+CH=15㎝と分かります。
展開図を描き「底面積」と「側面積」を出す
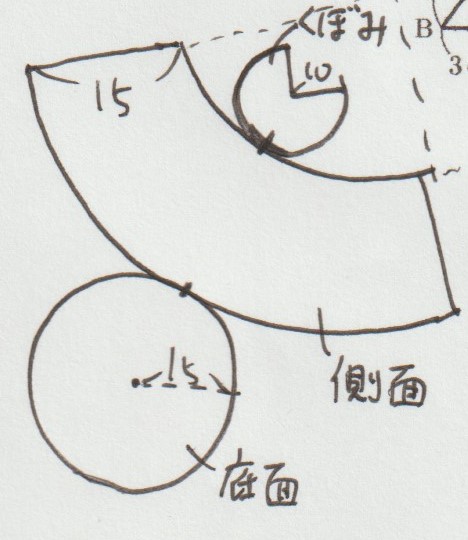
この問題の展開図は、上の図のようになります。
底面は「半径15㎝の円」となるので、面積は15×15×3.14 で出ます。
問題は側面の部分です。
側面の部分は「大きいおうぎ形から小さいおうぎ形を切り取った形」
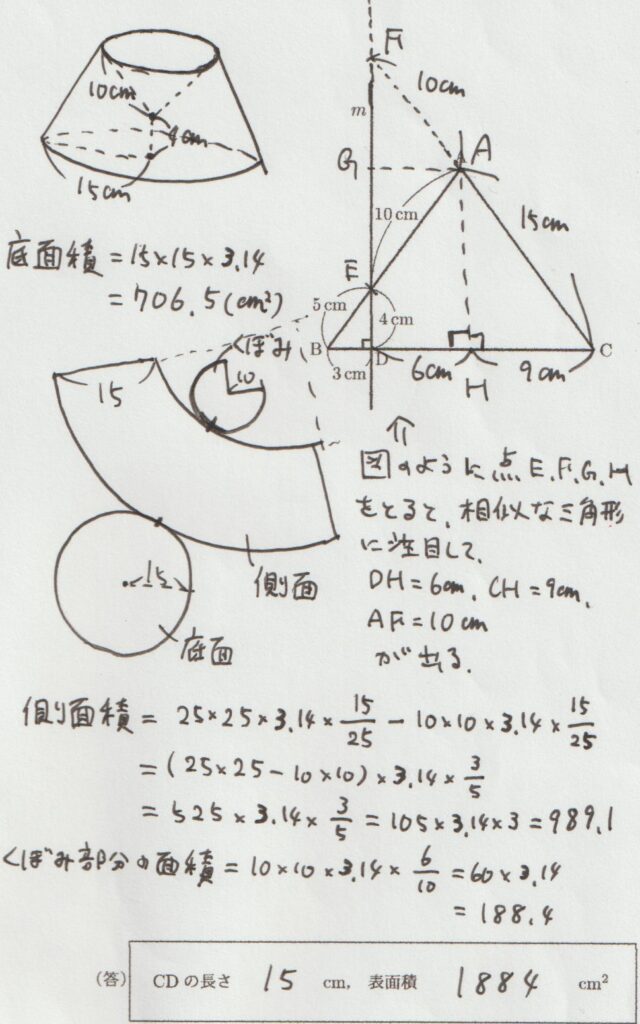
上の図を参考に、側面を形作る「大きいおうぎ形から小さいおうぎ形を切り取った形」について見ていきますね。
まず、もともとあった「大きいおうぎ形」は、上の図中のAFの長さが10㎝となることから、側面の面積は、以下の式で出すことができます。
25×25×3.14×(15/25)-10×10×3.14×(15/25)
くぼみ部分は「半径6㎝の円を底面とする円錐」の側面の面積と同じ
「くぼみ部分」とは、もう一度以下に示すように、「10㎝」の点線が描かれている部分を言います。

この「くぼみ部分」は「底面の円の半径が6㎝、母線が10㎝」の円錐の側面の面積を同じなので、くぼみ部分の面積は次の式で出すことができます。
10×10×3.14×(6/10)
表面積の問題に正解できるようにするための勉強法
このような回転体の表面積の問題をできるようにするためには、以下の2つのことを意識した上で勉強を進めていく必要があります。
必ず「でき上がった立体」と「展開図」を描く
できあがった立体がどのような形になるのかを、必ず描くことが大事です。
「上から見るとどう見えるのか」「正面から見るとどう見えるのか」を考えた上で、「全体としてどんな形なのか」が分かる図を描くようにして下さい。
このことに加えて、表面積を求める以上は「展開図」を描くことが最も重要です。
「底面、側面がどんな図形か」を考えることはもちろん、展開図において「組みたてたときに、どの部分とどの部分が重なるのか」を把握しておくことも大事です。
表面積とは「その立体を形作るすべての表面の面積の和」
「表面積って何のこと?」と生徒さんに聞くと、実はうまく答えられない生徒さんも多いです。
表面積とは「その立体を形作るすべての表面の面積」を「すべて足したもの」のことです。
ですので「こういう計算をすれば面積が出る」というものでもないのです。
だからこそ「立体を描き、展開図を描き、全ての面の面積をそれぞれ出す」というプロセスを、欠かせないわけなのです。
まとめ
鷗友学園女子中を受験されるにあたり「算数が心配」「基本はできるけれど、それより難しい問題ができない」など、算数の勉強でお悩みの方に向けて「中学受験対策フルサポートコース」をご用意しております。
鷗友学園女子中を受験する場合、中学受験の伝統的なテキスト「四谷大塚の予習シリーズ」に載っているような問題を「すべてできるようにすること」が受験対策の基本となります。
「予習シリーズ」で勉強されているお子さんはもちろん、中学受験大手の「SAPIX」の教材などで受験対策をされているご家庭からも、「算数が難しすぎる」というお声をよく聞きます。
このようなお困りことを解消するために「中学受験フルサポートコース」では「お子様の学力を引き出すこと」「ムダのない家庭学習のご提案」により、成績UPと志望校合格を目指します。
コースの詳細は、以下のリンクからご覧いただき、ご相談事がありましたら、まずは一度無料相談にお申し込み下さい。
