和差算は、中学受験算数の基礎とも言える単元ですが、小学校では習わないために、どう学習を進めていけば良いのかで悩むお子様もいらっしゃるかと思います。
この記事では、算数のプロ家庭教師として10年以上活動をしている鈴木が、和差算でお困りのお子様とその親御さんに向けて、和差算の全てを解説します。
和差算を難しいと感じているお子様は多いですが、その理由は「問題文の読み方が分かりづらいこと」「数量を線分に例えづらいこと」などが主な原因です。
実をいうと和差算は、これらのことを理解すれば (本当はもう少し大事なことはありますが) 、難しくないものです。
この記事では、和差算の基本から応用までを分かりやすく解説します。
また、よくある間違いや、問題を解くためのコツも紹介します。
この記事を参考に学習を進めていけば、お子様も和差算が「難しい」ものから「得意」なものへと変わるでしょう。
この記事が、その第一歩となることを願っています。
和差算の基礎基本

和差算とは一体何なのでしょうか?
そして、それが分かったとして、その先どんなことができるようになるのでしょうか?
これらの疑問に答えることで、和差算の基本を理解することができます。
この記事を読むことで、和差算の考え方を使って問題を解くためのヒントを得ることができます。
それにより、中学受験算数の文章問題を解く力が向上し、より高度な単元を理解することも可能になります。
和差算とは何か?
和差算は、中学受験算数の基礎基本ともいえる単元のうちの一つです。
中学受験に特化した塾に通うのであれば、小学4年生の段階で習います。
具体的には「2つの数量の差とその合計が分かっているとき、それぞれの数量を求める問題」を学びます。
例えば以下のような問題が典型的です。
例題 30個のみかんをAさんとBさんの2人で分けるとき、AさんはBさんよりも8個多く取りました。Bさんは何個取りましたか。
和差算の基本的な考え方
上のような例題では「~よりも・・・多く」などの文章から、和差算であることを見抜くことができます。
和差算であることが分かったら「みかんの個数」を線分図で表します。

和差算は「線分図で考える」という考え方を身につけるための題材とも言えます。
個数を線分図で表せたら、「2人とも同じ個数持っていたとしたらみかんは合計で何個あるか」を考えます。
これが和差算で一番大事な考え方です。
多い方に数を揃える
いま、Aさんの方が8個多くみかんを持っていますよね。
このときに「Bさんにも8個のみかんを追加した」と考えます。

すると、2人は同じ個数ずつみかんを持っていることになり、みかんの合計は38個となります。
この場合は「Aさん (数が多い方) の個数2セット分の合計」が38個なので、38÷2=19 (個) がAさんが取ったみかんの個数です。
Bさんはこれよりも8個少ないので、Bさんは11個となります。
少ない方に数を揃える
逆にAさんがBさんよりも多く取った8個分が「もともとなかった」と考えて、Bさんが取ったみかんの個数を求められます。
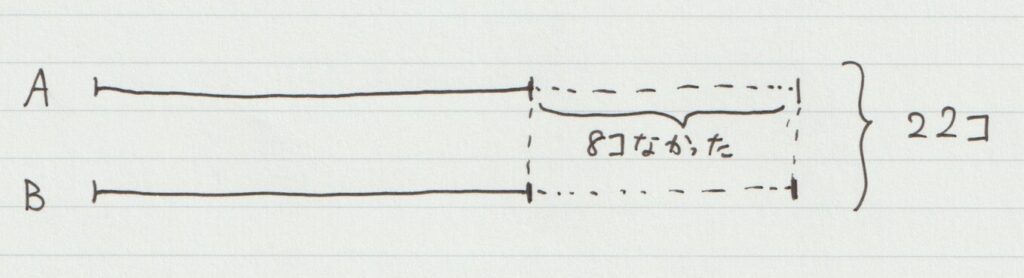
8個分が「もともとなかった」ので、みかんの合計は22個と仮定できますよね。
この場合は「Bさん (数が少ない方) の個数2セット分の合計」が22個なので、Bさんが取った分は22÷2=11 (個) となります。
和差算の基本公式
あくまでも、問題文を読んだ上で「和差算」であることが分かり「数を揃える」という考え方を受け入れられたのであれば、以下の公式が「和差算の基本公式」となります。
「多い方の個数」と「少ない方の個数」の和が▢、差が〇のとき、以下の式がなりたちます。
「多い方の個数」= ( ▢+〇 )÷2
「少ない方の個数」= ( ▢-〇 )÷2
ただこうした公式は、あくまでも「線分図」を描いて「ものの個数を線分の長さに例える」という見方ができた上で覚えておくことが大事です。
和差算の基本問題を解こう

和差算の考え方で解ける問題は、「2つの量の和と差」が分かっていることが大きな特徴です。
そのような特徴は、「人数、個数、時間、長さ・・・」などを求める問題で見ることができます。
先ほど和差算は「線分図を描いて考える」という考え方を身につける題材と書きました。
もう少し詳しくいうと、人数や個数のような量は「線分の長さ」で表現できることから、和差算の問題として出題されます。
そしてこの先「量を線分で表現する」「線分の差に注目する」という学習プロセスを通して、割合などを学ぶことになります。
ここからは、和差算の基本問題の解き方と解答例と共に紹介します。
これを読むことで、和差算の基本的な理解を深めることができます。
和差算の基本例題集
例題1. 人数の問題
4年3組のクラスの人数は32人で男子は女子よりも6人多いそうです。4年3組のクラスの女子の人数はそれぞれ何人になるか求めなさい。
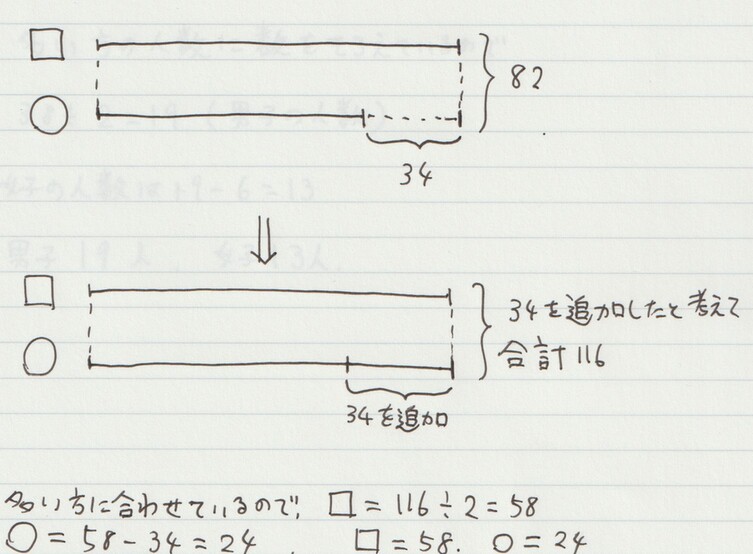
例題2. 数の問題
▢と〇の2つの数字があります。▢と〇を足すと82、▢から〇を引くと34になります。このとき▢の値を求めなさい。
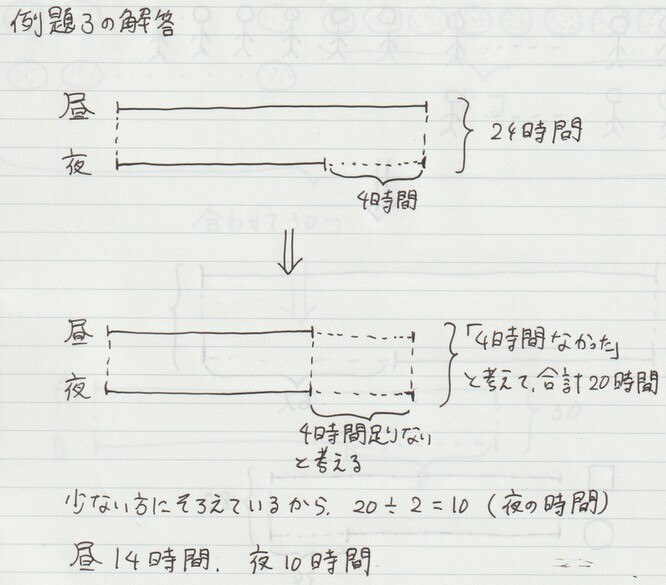
例題3. 時間の長さの問題
ある日の夜の長さは、昼の長さよりも4時間短かったそうです。この日の夜の長さを求めなさい。
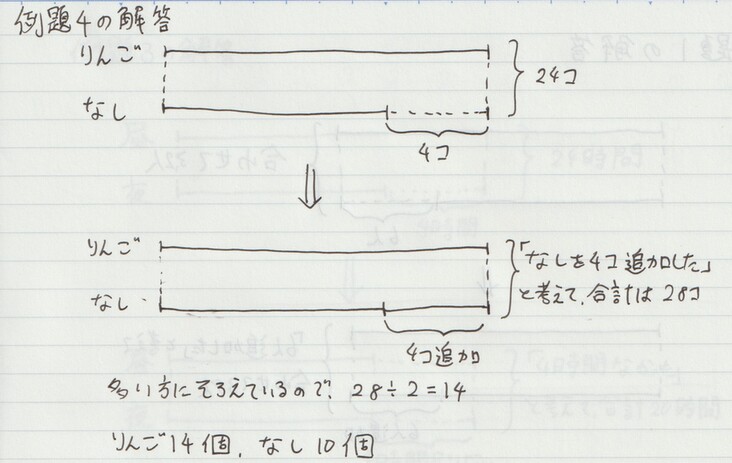
例題4. 個数の問題
りんごとなしが全部で24個あります。りんごの方がなしより4個多いです。りんごとなしはそれぞれいくつありますか?
例題5. お金の問題
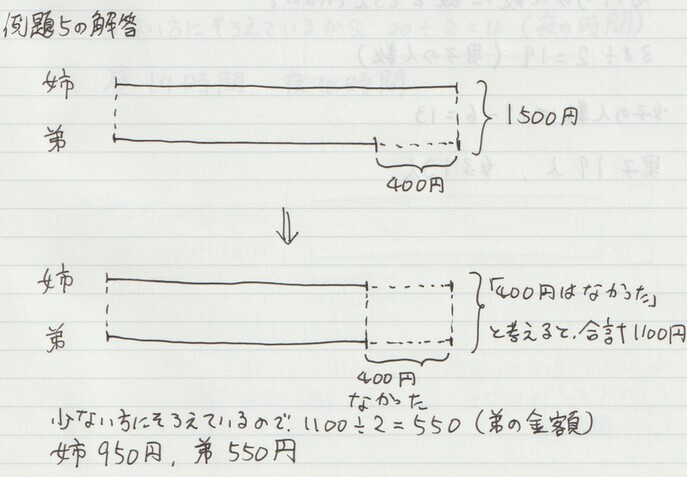
姉と弟が持っているお金の合計は1500円で、姉は弟より400円多く持っています。弟が持っているお金は何円ですか。
基本問題の解き方
1. 量を「線の長さ」に例える
これが小学生にとっては難しく感じることでもあるのですが、そもそも「量を線の長さ」と見ることから、和差算の問題を解くことが始まります。
「量」とはこれらの例題に出ているような「人数・時間・個数・金額」のことを指します。
これらを全て「線の長さ」で表現します。
2. 線分図を描く
実際に線分図を描いてみましょう。
このとき大事なのは、線分の「はしっこ」を揃えて描くということです。
そして、問題文に「・・・より多い」などの表現があるので、「どちらかの線分は長く (短く) 描く」という気持ちを大事にして下さい。
3. 数を入れる
線分を描いたら、数を書き入れていきます。
例題1の場合であれば、長い線分と短い線分の差の部分に「6」と書き、2本の線分の長さの合計を「32」としておきます。
他の問題も全く同じく、線分の差の部分に「4」、「5」などと入れておき、合計を「24」、「1500」などと書いておきます。
4. 数を揃える
和差算で大事なのは「差の分を追加したら (またはなくしたら) 合計はいくらか」という考えです。
例題5の場合だと、もともとの合計は1500円となっていますが「弟に400円追加したら、お姉さんの金額2セット分で、(架空の) 合計は1900円」と考えることができます。
他の問題も同様に「女子が6人追加されたら」「夜の長さが4時間増えたら」などと考えることで数を揃えて、「架空の合計」を出すことができます。
5. 合計を2で割る
何のために「数を揃えるのか」というと、最後に「架空の合計」を2で割って、それぞれの量を出したいからです。
最後はただ「2で割る」ということをしておくだけで、答えが出ます。
基本問題の解答
上記の「基本問題の解き方」に沿って作った解答がこちらです。

和差算を解くためのコツとポイント

ここからは、和差算のコツとポイントを解説します。
既に「基本問題の解き方」において、どのように和差算の問題を解くのかについてはお伝えしてきました。
ここからは解き方に加えて「この考えがあるから問題を解ける」というポイントを解説します。
線分図の使い方のコツを学ぶことで、和差算をはじめ、さまざまな問題も解けるようになるでしょう。
以下で解説することは、中学受験の算数全てにおける基礎基本ですので、ぜひ参考にして勉強されてみて下さい。
線分図を使った解き方のコツ
線分図を使って問題を解く際のコツについて、解説していきます。
線分の長さの「差」に注目する
まずは「線分の長さの差」に注目するクセを付けて下さい。
というのも、「和差算」という名がついているぐらいですので「和と差」の問題を扱うわけですが、その本当の目的は、割合や比の単元で「線分の長さの差」に注目して問題を解くためです。
ここで一つ、比の問題の例題を紹介しますね。
例題 ひろしさんの身長は、お父さんの身長の5/6で、その差は30㎝です。ひろしさんの身長は何㎝ですか。
こうした問題は、まずお父さんの身長を⑥、ひろしさんの身長を⑤とおいて、⑥-⑤=①=30という具合に「比の値1つ分 (線分の差) 」を出しておきます。
そうしておくことで、ひろしさん身長は30×5=150 (㎝) と出ます。
このような理由から、和差算を学ぶのは「割合と比」を理解するための布石なのです。
ないものを「ある」と仮定する
少し話がそれましたが、和差算では「ないものをある」と仮定することが一番大事です。
というのも、この考えがないと、問題が解けません。
先ほどの例題4を振り返ると、「なしを4個追加したら」という考えがなかったら、「りんごとなしが同じ個数ずつあって、その (架空の) 合計は28個」という考えにはならないです。
この考えがあるからこそ「りんごの個数2セット分で28個」という、「正解を出すためのヒント」が得られます。
和差算であることを見抜くポイント
さて、そもそも「和差算」であることが、どのようにして分かるのでしょうか。
線分図を描き、線分の差に注目して、「ないものをある」と仮定する問題だと、どのように分かるのでしょうか。
その答えは、この記事の初めにも少し書きましたが「・・・より~多い」などの文章から分かります。
というのも、このような文章は「・・・より~だけ長い」などと言い換えられるからです。
「男子が女子より7人多い」という文章であれば、男子を意味する「青い線の長さ」が、女子を意味する「赤い線の長さ」より7㎝長いと言い換えられます。
このような視点を持つことで、テストのときに「どの問題が和差算なのか」を見抜けるようになります。
和差算の応用問題も解いてみよう

和差算の基本はできても、応用問題が難しいと感じているお子様もいらっしゃるかと思います。
和差算の応用には、いくつか種類がありますが、典型的なのは「三つの数が出てくるもの」「他の単元と融合されたもの」などです。
このセクションでは、和差算の応用問題についても紹介し、三つの数の和差算の解き方や他の単元との融合問題の解き方を学びます。
これにより、和差算の理解を深め、成績UPにもつながるような問題にも対応できるようになるでしょう。
三つの数の和差算の解き方
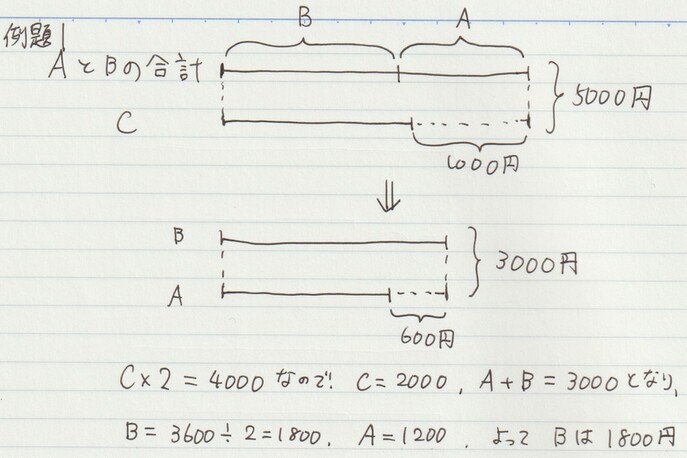
例題1. A、B、Cの3人が合わせて5000円持っています。AとBが持っているお金の合計は、Cが持っているお金より1000円多いです。また、BはAよりも600円多く持っています。Bが持っているお金は何円ですか。
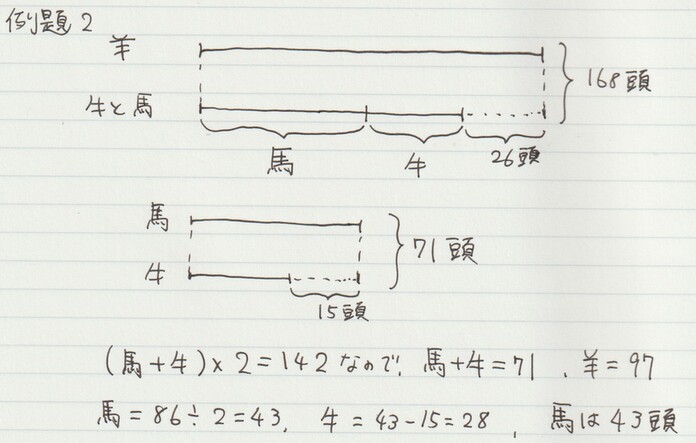
例題2. 牛、羊、馬を合わせて168頭かっています。羊が最も多く、その数は牛と馬を合わせた数よりも26頭多いそうです。また、牛が最も少なく、その数は馬よりも15頭少ないそうです。馬は何頭かっていますか。
線分図をつなぐ
数が3つの和差算では、線分図をつなぐことで「3つの数のうち2つの数の和」を求められます。
例題1も例題2も、以下のような線分図を描くことができます。
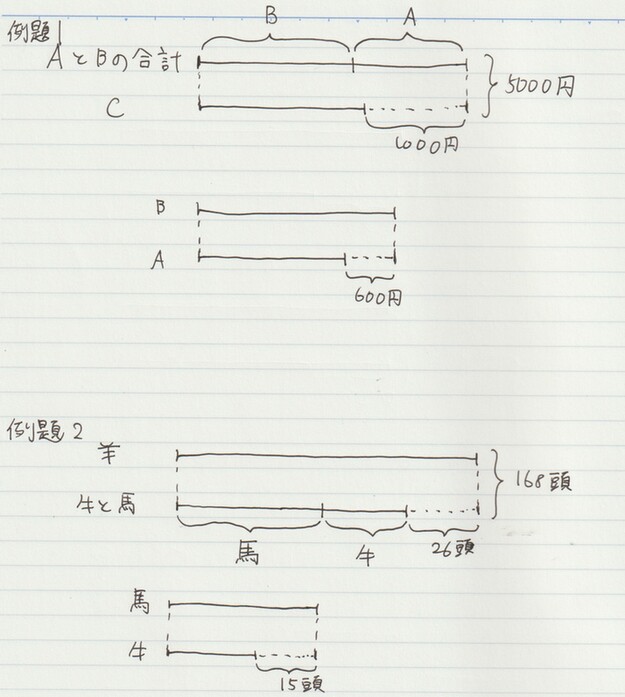
例題1では、Cよりも「AとBの合計の方が多い1000円分」がなかったとして、「Ⅽの金額2セット分」で4000円であることが分かります。
同様に、例題2では「26頭分いなかった」として、「牛と馬の合計2セット分」で142頭であることも分かります。
このようなことは、最初に書いた通り「線分図をつなぐこと」で分かります。
どの線分同士をつなぐのかは、問題文を振り返ると分かります。
例題1では「AとBが持っているお金の合計」、例題2では「牛と馬を合わせた数よりも~」とありますので、これら2つの数を表す線分同士をつなげば良いのです。
解答がこちらです。
他の単元との融合問題の解き方
平均との融合問題
例題3. お父さんとお母さんとかず子さんの年齢の平均は28才です。お父さんはお母さんよりも6才年上で、かず子さんはお母さんが27才のときに生まれました。お父さん、お母さん、かず子さんの年齢はそれぞれ何歳ですか。
平均を習ったあとに、和差算との融合問題を解くこともあります。
この問題の場合、3人の年齢の平均が28才とありますよね。
中学受験では「平均から合計を出す」という考え方が必須ですので、これを使うと「3人の年齢の合計は84才」となります。
これが分かれば、あとは以下のように考えれば正解できます。

差集め算の初歩の問題
例題4. マジックとボールペンを5本ずつ買うと代金は750円になります。マジック1本の値段がボールペン1本の値段より20円高いとき、マジック1本は何円ですか。
この問題は、「差集め算」といって、2つの量の差の合計に注目して、和差算の考えで解くタイプの問題です。
まずマジックとボールペンを1本ずつ買うと、マジックとボールペンの金額の差は20円です。
2本ずつ買うと、「マジック2本分の金額」と「ボールペン2本分の金額」の差は40円です。
3本ずつ、4本ずつと考えてみると、5本ずつ買った場合のことが分かってきます。
5本ずつ買うと、「マジック5本分の金額」と「ボールペン5本分の金額」の差は100円になります。
ここで「5本ずつ買ったときの合計」が分かっているので、和差算で解けるわけです。

四角形の問題との融合
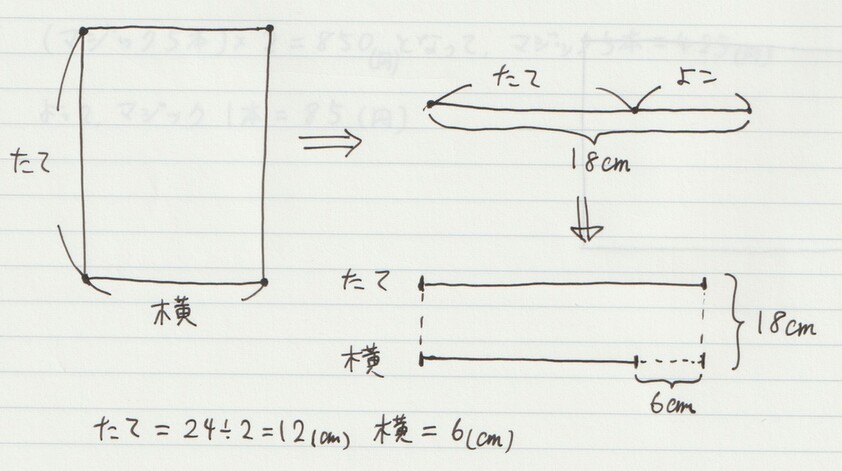
例題5. まわりの長さが36㎝で、たての長さが横の長さより6㎝長い長方形があります。この長方形の横の長さは何㎝ですか。
こうした問題も、和差算で解くことができます。
まわりの長さが36㎝とあるので、たてと横の長さを足すと、18㎝になりますよね。
しかも「たての長さが横の長さより6㎝長い」とあるので、以下のような図を描いて答を出せます。
和差算の発展問題にも挑戦しよう

和差算の「応用問題」と「発展問題」は、お互いにどう違うのでしょうか。
あまり気にすることでもないのですが、応用は「他の単元の問題を解くのに、考え方を応用する」という考えで大丈夫です。
発展は、和差算の問題を解く考え方そのものが「発展したものである」ととらえて良いと思います。
例えば以下では「合計の分からない三つの数」を出す問題を見ていきますが、数が増えても「まずは全て足す」ということをします。
合計が分からなくても、このような考え方が使えることもあります。
このセクションでは、より複雑な和差算の問題を解くための方法を学びます。
三つの関係が与えられた和差算
例題1. AはBよりも大く、BはCよりも大きいとします。AとBの和が36、AとBの差が4、BとCの差が9であるとき、ABCはそれぞれいくつですか?
このような問題は、まず「和と差の関係」が明らかになっているものを探します。
すると「AとBの和と差」が出ているので、まずはAとBの値が出そうですよね。
BはAよりも「4だけ小さい」ので、線分図を描き「Bが4つ追加されたら・・・」などと考えることで、「A =40÷2=20、B=20-4=16」となります。
最後に、BはCよりも大きいので「C=16-9=7」となって、全ての答が出ます。
合計が書いていない和差算
例題2. 3つの数ABCがあります。AとBの和が21、BとCの和が19、AとCの和が34の時、ABCはそれぞれいくつですか?
このような問題もたまに見ます。
問題をよく見ると、問題文中に「A、B、C」が2回ずつ出てきてますよね。
このように、同じ数が複数回ずつ出てきたときは、思いきって「全て足す」という考え方もあります。
数を全て足す
「A+B」+「B+Ⅽ」+「A+C」=21+19+34=74となりますよね。
そして、ここからお伝えすることは、数の性質をよく知っていることが前提なのですが、「A+B」+「B+C」+「A+C」というのは結局、「A+B+C」+「A+B+C」のことです。
というのも、足し算では「足す順番」を入れかえても大丈夫なわけです。
三つの数の合計を出す
ということで、「A+B+Ⅽ」という数2つ分で74ということが分かり、A+B+C=37となります。
「ここからどうしよう・・・」となってしまいそうですが、問題文を振り返ると「AとBの和が21」「BとCの和が19」とありますよね。
これらをまたさらに足すと「A+B+B+C」=40となりますが、何か気づきませんか?
余分に足したものを見つける
「A+B+B+C」という式を見ると「A+B+C」に、Bを余分に足したものになっています。
ですので、37にBを足して40なので、B=3ということが分かります。
このことから、A=18、C=16となります。
確かめもお忘れなく‼
A、B、Cが全て出ましたが、問題文の条件と同じになりますか?
答が出たら、最後は必ず、実際に「A+B」「B+Ⅽ」「A+C」を計算してみて、合っているかどうかを確かめてみて下さい。
和差算でつまづきやすいポイントとその改善策

お子様の様子を見ていて、和差算に限らず「こんなところでよくミスしてしまうな」と感じるところはないでしょうか。
和差算は、中学受験算数の基礎とは言え、その基礎こそが実は難しい部分を多く含んでいます。
ですので、お子様にとって「つまづきの原因」になってしまう要素も、和差算には少なからずあります。
和差算でつまづくポイントは、主に以下の5つです。
・そもそも和差算だと気づかない
・「線分の長さ」に例えられない
・数を揃えられない
・大小関係を間違う
・求める答を間違える
ここからは、こうした「つまづき要素」に対して、どのように気をつければ良いのかについて解説します。
それぞれ対策を見ていき、苦手を得意に変えるための参考にしていきましょう。
そもそも和差算だと気づかない
1回和差算を習っていても、例えばテストで「他の単元の問題と同時に」和差算の問題が出題されたときに、出てきた問題が和差算だと気づかない場合もあります。
原因としては「忘れている」「問題文の読み方まで含めて学習していない」ということも考えられます。
対策としては、週に一度小テストのようなプリントを利用して、「習ったことを思い出す練習」が必要です。
また、この記事でも書いたように「・・・よりも~多い」という文章に注目することで、和差算だと気づきやすくなります。
「線分の長さ」に例えられない
小学生のお子様にとっては、ものの個数などを「線分の長さ」と見ることに違和感を持つこともあります。
実をいうと小学2年生の段階で、算数においては「テープ図」という名のもとに、量を線分の長さで表現することを学びます。
しかし「ものの個数は個数であって、線の長さなどではない!」と思ってしまうことも、珍しいことではありません。
そんなときは、まずは具体的な絵を描き、絵に描いたものが「どうせ鉛筆で描くのだから、線で描いて表現しても問題ない!」と思えるまで、まずは絵で表現することも対策の一つです。
数を揃えられない
「ないものをあると仮定して数を揃える」という考えが一番大事なのですが、お子様にとっては受け入れづらいものになっている場合も多いです。
というのも、中学受験の算数を学ばない限り、このように「何かを仮定して、ありもしないことを考えて問題を解く」ということはしません。
りんごがなしより4個多いとき、そのような現実がもしあるのだとすれば「仮になしを4個追加したら・・・」などと、日常でも考えませんよね。
お子様にとっては「何が現実で、何が仮定なのか」を区別することが、年齢的にも経験的にも難しい場合があります。
もし、お子様にとって「数を揃える」という考えが非常に分かりにくいものであれば、まずは「基本問題だけを、解き方を覚えて解く」という方法で勉強しても構いません。
大小関係を間違える
生徒さんの様子を見ていると、大小関係を間違えてしまうことがよくあります。
例えば例題1では「男子は女子より6人多い」とありますが、線分図を描けたとしても「女子が男子より6人多いことになっている」ということもたまにあります。
このようなことを防ぐために、問題文を振り返り「自分の描いた線分図は正しいかどうか」を確かめるという気持ちを持つことが大事です。
もっと細かい話をすると、このように「問題文に書いてあること」と「自分が描いた図」との間に、違いがないかどうかを確かめておくことが、見直しのポイントの一つです。
求める答を間違える
お子様の様子を見て「問題文で問われていることとは違うこと」を答えてしまうという場面はないでしょうか。
例題2であれば「▢の値」とあるのに「〇の値」を求めてしまったり、例題5だと「姉の金額」を求めてしまうことなどがあてはまります。
このようなことを防ぐために、ここでも「問題文を振り返る」という気持ちが大事になってきます。
また、答を出すために「数を揃える」「合計を2で割る」というプロセスを先ほど書きましたが、常に「今計算して出てきた数字は何を表すのか」を振り返ることも重要です。
図を描くなどの「目に見える行動面」だけではなく、お子様の中にある「他の人からは見えない思考面」が正しいかどうかも確かめられると、お子様は間違いなく正解できるようになります。
成果が出る家庭学習の進め方

和差算を解くのに必要な考え方を身につけるためには、どのように学習していけば良いのでしょうか。
これまでは、具体的な例題とその解説を通じて、和差算の問題を解くための大事なポイントなどについて解説してきました。
しかし、一番大事なのは、そのような大事なポイントなどの「この記事にて書かれていたこと」を、お子様ご自身ができるようになることです。
ここからは、それを叶えるための家庭学習の方法について解説します。
同じ問題を解く
まずは解説を読んだり聞いたりして「分かったな」と思った問題を、もう一度一人で解き、正解を出せるようにして下さい。
集団塾に通っていると、先生が最初に問題を解説してくれますよね。
「先生ができること」を、まずは「自分もできること」に変えることが大事です。
数値替え問題を解く
「同じ問題」に正解できたら、次は「数値替え問題」を解きましょう。
いわゆる「類題」というものです。
例えば、この記事で出てきた「お金の問題」がありましたよね。
「合計1500円、姉と弟の金額の差が400円」という問題でしたが、今度は「合計2000円、差が600円」などの問題を解きましょう。
正解できた理由を見つける
ただ「同じ問題と類題を解く」というだけではなく、正解を出す過程において、「こう考えるからこそ正解を出せた」と思えるポイントを見つけてみて下さい。
逆にいえば「これをしなかったら正解を出せない」というポイントのことです。
和差算においては「ないものをあると仮定する」という考えがなかったら、正解を出せません。
考え方をマネする
実をいうと和差算だけではなく、他の単元の問題でもそうですが、「正解できた理由」というのは、「どんな問題を解く際にも出てくる共通のポイント (考え方) 」とも言えます。
この記事で出てきた「りんごとなし」の問題では「なしを4個追加したら」と考えましたよね。
クラスの人数の問題では「女子がさらに6人いたら」と考えました。
このような考えが共通していることからも分かるように、「・・・より~が〇〇多い」などの文章が問題文にある場合は「・・・が〇〇追加されていたら」という考えを「マネする」と良いのです。
何も見ないで正解を出す
例題、類題はもちろん、「考え方」をマネして解ける問題は全て、「解説など何も見ずに正解を出すこと」が大事です。
問題文を読み、和差算であることに気付いた上で、実際に和差算の考え方を使って正解できてはじめて「理解できた」「身についた」と言えます。
このプロセスまで実行しないと「勉強した」とは言えないのです。
他の単元の問題と同時に出題
和差算の問題に正解できてきたら、他の単元の問題も同時に載っている「総合問題のページ」などを利用して、「テスト形式」の問題演習を行いましょう。
「テスト形式での問題演習」とは、「どの問題がどの単元に属するものなのか」を判断する練習まで想定して問題を解くことです。
問題集のページを開き「和差算」と書いてあったら、当然そのページに載っている問題はすべて「和差算」で解くことが分かりますよね。
しかし、大事なのはテスト本番で、問題文を読んだときに「これが和差算だ!」と判断した上で、実際に正解できることです。
よく「普段はできるのに、テストでは点が取れません」というご相談がありますが、この「テスト形式の問題演習」ができていないことが主な原因です。
ぜひ、他の単元の問題も同時に出題して、問題を解いてみて下さい。
和差算が難しいと感じる方からよくある質問

和差算の無料プリントなどはありますか
インターネット上に、無料で問題とその解説を提供してくれているページもあります。
「さくさく文章題」というページで、基本問題を100問以上ダウンロードできます。
基礎を繰り返し練習したい方におすすめです。
和差算を理解するのにおすすめの教材はありますか
和差算単独で学習をしたいときは、以下の「思考力算数練習帳シリーズ」がおすすめです。
応用問題や発展問題を理解するにはどうすれば良いですか
基本的な問題を理解するプロセス同様に、「典型的な応用問題」「典型的な発展問題」を題材として、「難しい問題を解くのに必要な考え方」を身につけていくことが大事です。
例えばこの記事で、三つの数が出てくる和差算を紹介しましたよね。
このような例題を題材として、先ほどの「成果が出る家庭学習の進め方」にそって、とにかく「解説など何も見ないで正解を出すこと」ができるまで練習して下さい。
こうした「思考と行動の繰り返し」によって、応用問題もできるようになります。
和差算を得意にする勉強法まとめ
この記事では、「和差算が難しい!」とお困りの方に向けて、和差算を得意にするための具体的な方法を徹底的に解説しました。
和差算は、中学受験算数の基本であり、理解していないと高度な単元に進むことが難しくなります。
しかし、正しい理解と練習方法を身につければ、必ず理解できます。
この記事では、まず和差算の基本とは何かを説明し、その理解を深めることが重要だと述べました。
次に、基本問題の解き方と練習問題の解答例を提供しました。
これにより、和差算の基本的な考え方を身につけることができます。
さらに、和差算でつまづきやすいポイントとその改善策についても詳しく解説しました。
よくある間違いとその対策、線分図を使った解き方のコツなど、和差算の理解を深めるための具体的なアドバイスを提供しました。
最後に、和差算の応用問題と発展問題についても解説しました。
これにより、三つの関係が与えられた和差算や他の単元との融合など、より複雑な問題に対する解法を学ぶことができます。
和差算は難しく感じるかもしれませんが、正しい理解と練習方法を身につければ、必ず理解できます。
お子様が和差算を得意にするために、ぜひこの記事を活用してください。
