こんにちは。算数・数学専門家庭教師の鈴木です。
今日は中学受験を目指す生徒さんが、どのように予習シリーズを活用して「割合」の苦手を克服してきたのかについて、解説をしていきたいと思います。
予習シリーズを使って中学受験の勉強をしている方は、4年生の2学期に初めて「割合」を習いますよね。
そこで出てくるのは「もとにする量」「比較量」など、一見すると難しい単語と、難しそうな文章問題です。
あとでも書きますが、「倍」の考え方が理解できていないと、割合を理解することは難しいのです。
生徒さんも、初めは「倍」がよく分からない様子でしたが、ここに書いてある方法で勉強をしてきた結果、生徒さんの成績も上がり、こおような嬉しいご報告もいただきました。
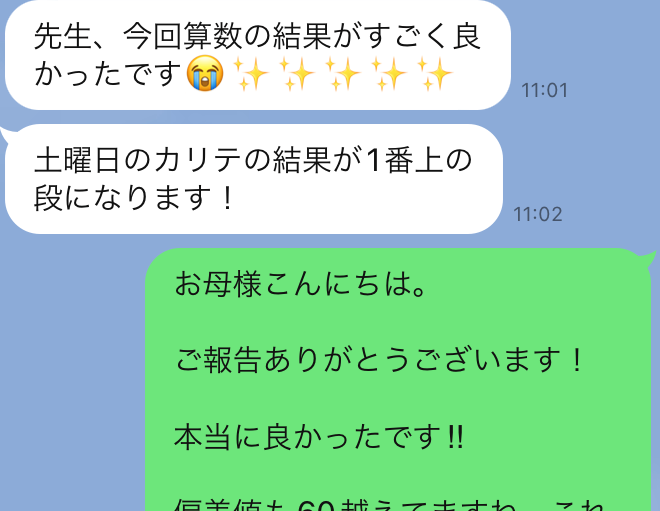
「倍がよく分からない」「問題文も難しい」と思っていた生徒さんが、どんな風に「予習のシリーズの練習問題」を解けるようになったのか、以下で詳しくお伝えしていきます。
確実に成果の出る勉強法ですので、「割合」が苦手だという方は、もう一度この記事も参考に勉強されると、成績UPも間違いありません。
予習シリーズ4年で習う割合の内容
予習シリーズの4年下巻においては、「割合」と言っても「%」や「~割・・・分」などを学ぶわけではなく、「~の・・・3分の2」など、「もとになっている量をいくつに分けたうちの何個分か」という考え方を学びます。
例えば「1500円の2/3」と問題文にあったら、「1500円という金額を3等分したうちの2つ分」という読み方をします。
このように4年生の段階では、予習シリーズで「割合を分数で表すこと」を主に学びます。
割合でつまずく理由
以下では中学受験生でなくても、「割合でつまずいてしまう主な理由」について解説していきますね。
こちらの記事でも詳しく書いておりますので、ぜひともご一読いただけると嬉しいです。
https://sugaku1bann.com/2022/03/07/wariainonigatetaisaku/
「~倍」が分かっていない
「父の年齢が花子さんの年齢の2倍」と問題文に書いてあったら、「 (花子さんの年齢) ×2= (父の年齢) 」という式を立てることになります。
ところが「~倍」という文章が「式としてどのような意味になるのか」が分からないと、割合を理解することができません。
というのも、上に書いた例文を割合 (分数) を使って書き表すと「父の年齢の1/2が花子さんの年齢」となり、ここで「年齢の2倍」という考え方を使うからです。
分数の理解不足
上に書いたような「1/2」などが、「分数の記号を使わずに説明できるかどうか」で、分数が理解できているかどうかが分かります。
「1/2」というのは「2等分したうちの1つ分」となりますが、もしお子さんが割合に苦手意識を持っていたら、このような説明ができるかどうかを確かめる必要があります。
「もとにする量」「くらべる量」が分からない
「もとにする」などというと、4年生のお子さんにとっては難しい表現だと感じることも多い印象です。
ですので私は「もとにする」という表現を最初にせずに、「全部と一部」という表現で、問題文の解説などもしていました。
「花子さんが1500円持っていて、その2/3を使って・・・」という問題文があれば、「全部で1500円」「使った一部の金額が何分のいくつ?」などと伝えてみることで、生徒さんは「割合の式の立て方」も分かってきました。
「もとにする量」「くらべる量」が分からないとき、「お子さんにとって受け入れやすい表現」に言い換えて理解してもらうという視点が大切です。
線分図が分からない
中学受験の算数ではどうしても、線分図を使って問題を解くことが求められます。
これは何かというと、「ものの個数」「年齢」などの量を、「線分の長さ」に例えて解くというものです。
問題文の中で、「~より多い」「~の2倍より・・・少ない」などの表現があれば、長い線分と短い線分を描き、2つの線分の「和や差」に注目して解くことが、中学受験の算数では必須です。
割合においても例外ではなく、そもそも割合が「倍」を言い換えたものである以上、線分図を描いて「線分をいくつに分けたうちの何本分か」を考える場面があります。
このような「線分による例え」が分からないと、どうしても割合の問題を解くことができません。
割合を理解するために必要なこと
どんな生徒さんも、まずは「倍」の復習からすることをおすすめします。
10cmのえんぴつAと6㎝のえんぴつBがあるとき、「BはAの何倍の長さか」というような問題を正解できるかどうかを、確かめられると良いと思います。
このような問題を題材として、「Aをもとにしたとき、Bの割合はいくらか」と聞かれることは「BはAの何倍か」を聞かれることと同じであることを学びます。
こうして「割合と倍」が理解できてきたら、実際に予習シリーズのテキストの必修例題から解いていきます。
まずは必修例題の復習から

必修例題を解き、問題文の読み方、式の立て方、見直しの仕方などを身につけていくことが大事です。
上のような例題だと「40人」がもとにする量、「6人」がくらべる量であると読めているかどうかを、生徒さんの考えも聞きながら確かめていくことになります。
このようにして一緒に問題を解いた後は、必修例題のすぐ次に載っている「類題」を、生徒さん一人だけの力で解いてもらいました。
必修例題の次に必ず類題を解く

数値変え問題などと言いますが、問題文の文章構造は変えずに、数値と単語のみ変えた問題を「必修例題を解くときに使った解き方」をマネして解くことが大事です。
授業を聴いて、「解説が理解できたな」と思ったら、その解説をマネして解くことができる類題を、今度は解説など何も見ずに「自分で最後まで正解を出すこと」をするように、お子さんにも伝えて下さい。
基本を身につけるためにも、この勉強プロセスは欠かせません。
基本問題を身につけるための演習問題集の使い方
予習シリーズには、各塾さんで授業の際に使うテキストと「演習問題集」があります。
テキストのみだと、どうしても問題演習量が確保しきれないという声もあります。
以下では、テキストの基本問題レベルの問題をできるようにするための「演習問題集」の使い方についてもお伝えしていきます。
基本問題を全て正解できるようにする

演習問題集には、各単元において「基本問題」が載っているページが2ページ必ず用意されています。
テキストにて基本問題をできるようになってきたら、演習問題集の基本問題のページを開き、「似た問題を全て正解できるようにすること」が大事です。
マルつけの仕方はどうすれば良い?
テキストの基本問題を全て正解できる自身があるお子さんは、ページ内の全ての問題を解いてからマルつけをするのがおすすめです。
そうすることで、特に四谷大塚さんに通っているお子さんなどは、おうちで週テストの練習をしていることにもなります。
テキストが難しく感じているお子さんは、「1問解いてマルつけ」を繰り返すか、「3問ずつ解いてマルつけ」をするのもおすすめです。
そうすることで「間違った考え方のまま同じような問題を解くこと」を防げますし、もし本当に間違った考えで解いていたのであれば、マルつけをするごとに「正しい解き方」を知るきっかけもできます。
できた問題こそ振り返る
できた問題はそのまま「できたから次にいく」というスタンスをとらずに、「なぜできたのか」「正解できるポイントが何なのか」を振り返ることが大事です。
実際に私の授業でも、できたら必ず「どう解いたか教えて!」と生徒さんに聞いています。
こうした振り返りをすることで、「たまたま答が合っていただけ」という状況になっていないかどうかも確かめられます。
そして何より、「どんな問題を解く際にも出てくる共通のポイント」を見つけることができ、そのことが結果として「考え方を身につけること」にもつながります。
できなかった問題の直し方

「正解を出したのに間違っていた問題」は、そもそも「問題文をどう読んでいたか」まで振り返ってみて下さい。
例えば上の❻のような問題ができていなかった場合、「480円」が、「割合の言葉を使うと何になるのか」を振り返ることが大事です。
この480円は「くらべる量」となりますが、そのように読めていなかった場合、「文章中のどの表現に注目して、そう読むことが分かるのか」を、「必修例題」なども振り返りながら知ることが大事です。
この他にも「問題文の読み方は合っていたが、式の立て方が違う」「式を計算した結果が違う」などの原因が浮かび上がるのではないかと思います。
そのようなときは、「ここでは自分が書いた式が正しいかどうかをチェックする」などのように、「どのタイミングで、何をすることが見直しなのか」を、お子さん自身が気づけるように、お声をかけてあげて下さい。
類題を探してもう一度チャレンジ

できなかった原因が分かったら、「正しい問題文の読み方を知る」「見直しの仕方を知る」などのように、「間違いなく正解できるようにするために必要なこと」を実践していきます。
先ほどの❻番のような問題をもう一度解き直したら、次は上の■6のような類題をすぐに解き、正解できるかどうかを見ていくことになります。
演習問題集を開くと、先にもお伝えしたように、基本問題が載っているページは、各単元につき2ページ分あります。
そのうちの1ページから、「できなかった問題の類題」を探して、実際に正解できるように練習していくことが大事です。
練習問題を身につけるための問題集の使い方
ここからは、基本問題をできるようになってきた後に、少し難しい練習問題もできるようにするためのステップについて解説していきます。
と言っても、今までお伝えしてきた勉強方法と全く同じ方法で「できなかった問題」を「できる問題」に変えていくこといなります。
基本問題の身につけ方と実は同じ

テキストを開くと、基本問題の次のページに「練習問題」のページがありますよね。
上の③は、実際に演習問題集に載っている練習問題の一つです。
「練習問題」は「基本問題」と違い、「数値を変えただけ」のような問題が、テキストの中だけでは見つけにくいこともありますが、演習問題集を開くをすぐに見つかります。
先ほど「演習問題集には各単元において基本問題のページが2ページ」と書きましたが、実は練習問題のページについても、全く同じことが言えます。
ですので、もし仮に上の③のような問題ができなかったのであれば、「問題文の読み方」「見直しの仕方」を振り返り、再度以下の (2) のような問題を解くことになります。

このようにして問題演習していくことで、練習問題もできるようになっていきます。
基本問題との決定的な違い

基本問題と練習問題を比べたときに、割合の問題においては以下のような違いがあります。
◆基本問題◆
文章中に「もとにする量」「くらべる量」がすぐに分かる形で出ている
◆練習問題◆
文章を読み「もとにする量」「くらべる量」を自分で設定する
例えば上の (2) の問題だと、カサが750円というわけではなく、「残ったお金が750」となっています。
ということは、もっていたお金の2/7が750円ではなく、「3/7」が750円となりますよね。
このようにして、この問題では「くらべる量の割合がいくらか」を、問題文を読んだ上で「自分で設定する」というプロセスが必要になります。
ここが「基本問題」と決定的に違うところです。
テストの点数UPのために解くべき問題
以下では「点数UPのためには必須の演習問題」についてお伝えしていきます。
これらは全て「練習問題」の類題なので、これまでお伝えしてきた勉強方法によって、その解き方も身につきます。
実際に生徒さんも成果が出ました。
線分図を描かないと分からない問題

このような問題も、演習問題集には最低でも2問ずつ載っています。
この問題は、なぜ線分図が必須かというと、問題文中に「~より40円少ない」とあるからです。
線分図を描き、線分の長さの「どこからどこまでが全体の何分のいくつで、何と何の差が40円なのか」を考えないと、正解することが難しいです。
こうした問題も正解できるようになると、割合だけではなく「どんなときに線分図を描けば良いのか」も理解できてきます。
棒の長さの問題は必須

これと似た問題が、5年生以降で学ぶ「比」でも出てきます。
この問題では、数字が同じでも、その数字が何かの割合にあたる量を表すとき「もとの量はお互いに違うかもしれない」という考え方を学ぶことになります。
こうした見方も身につくと、その先算数の理解が進みます。
はね返るボールの問題も必須

この問題はほぼ毎年の「カリキュラムテスト」「組み分けテスト」などで目にします。
それだけ頻出の問題ですし、実際にこの間も出ました。
最初は生徒さんも「この問題できない」と言っていましたが、この記事で解説してきた勉強法によって、自分一人で正解できるようになりました。
「例題の解説を聞いた (読んだ) 後は、すぐに類題に取りかかる」を繰り返したのが良かったと、私も実感しています。
点数UPを実現する家庭学習のやり方
この記事の最後に、簡単に「家庭学習において大事なこと」を2つ、紹介していきますね。
これらを実践できれば、成績UPも夢ではないです。
「できるようになった問題」の類題は毎日やる
「基本問題」「練習問題」に限らず、「それまでできなかったけれど、できるようになった問題」は毎日解くことで、記憶に残るようにすることをおすすめします。
そうすることで、考え方のみならず「見直しの仕方」なども身についてきます。
解説は原則見ない
当然のことのように思えますが、お子さんにとっては「何も見ずに、過去に出てきた考え方を思い出す」という思考が、難しいと感じることもあります。
ですので、ここであえてもう一度「ヒントなど何も見ずに正解を出す重要性」をお伝えします。
これを乗り越えれば、繰り返しになりますが、成績UPも夢ではありません。
これらの学習方法をとった結果・・・

はじめは算数に苦手意識しかなかった生徒さんでしたが、「四谷大塚の公開組み分けテスト」で、それまで「110点取れたら良い方」だったのが、146点も取れました。
ここでお伝えしてきたことは、本当に再現性の高い方法です。
割合だけではなく、その先に続く「立体の体積」「一方にそろえて解く問題」などでも「できなかった問題」が「できる問題」に変化しています。
ぜひこの記事も参考に、問題演習をすすめてみて下さいね。
