算数のテストで点数を上げるための見直しの仕方

こんにちは。算数・数学プロ家庭教師の鈴木です。

これまで以下の記事で、「計算ミス」や「ミスの種類」とその原因、「そもそもミスとは言えない実例」について述べてきました。

計算ミスの正体を知りたい方は、こちらの記事をご覧下さい。

https://sugaku1bann.com/2021/10/25/keisannmisunogenninntotaisaku

ミスの種類について知りたい方は、こちらもご覧下さい。

https://sugaku1bann.com/2021/10/28/kearesumisunoshoutai/

お子さんはミスをしているのではなく、「正解したつもり」になってしまっているという考え方については、こちらにまとめてあります。

https://sugaku1bann.com/2021/10/26/misudewanakuseikaisitatumori/

思い込みや勘違いが原因で正解できていないのであれば、「正しい知識を取り入れること」からしなくてはなりません。

その場合は、あとでも述べるように、「教科書の基本例題を解くこと」「例題を解くことで考え方を学ぶこと」などが、正しい知識を得るためには必要です。

ここでいう正しい知識とは、これまで述べてきた「問題文の読み方や記号の意味とその使い方、何をもって正解と言えるのかなどを理解していること」を指すとします。

ここからは、ひとまずそういった正しい知識を得ているという前提で、「本番のテストにおいてミスを防ぐためには何ができるのか？」という考え方を軸に、見直しの目的とタイミングについて、書いていきたいと思います。

そもそも「見直し」とは何か？

まずは「見直しとは何か？」といったことから述べていきます。

これについては、答は割と簡単で「答が合っているかどうかを確かめる行動」ということになります。

ですので、先に大切なことを言うと、合っているかどうかを確かめられないものについては、そもそも見直しの概念はありません。

もう一つ大切なことは、「答が合っている」と一言で言っても、その言葉は広い意味を持つ場合が、多くあるということです。

大きく分けて二つの意味がありますが、一つは「自分が納得できている」という意味で答が合っているということです。

もう一つは「テストを採点する人の採点基準を満たす」という意味で、答が合っているということです。

実は多くのお子さんが、「自分が納得できているかどうかを確かめる」という意味で、見直しができていることも多いのですが、「採点する人の基準」まで考えて見直しができていない結果、テストでは思ったほど点数が取れていないということがあります。

ですので、「見直しをすることとは、具体的に何をすることなのか？」を考えたときに、「テストを採点する人にとって、自分が書いた答案はどう映るのか」まで見据えて、見直しの仕方を考えていく必要があります。

このことは特に、中学以降の定期テスト対策をする際に、大切になる考え方です。

まとめると、見直しとは、以下の二つの意味を持つものであると、考える必要があります。

・自分が考えたことや、書き出したことなどが合っているかどうかを確かめる行動

・「テストを採点する人」が思う正解の基準に合わせて、答案が作れているかどうかを確かめる行動

動画でも解説しております。

https://youtu.be/CicdGO4IZqk

見直しをかけるタイミングを知ることが大事！

ここからは、見直しをかけるタイミングについて、お話していきます。

ここでいう「タイミング」とは、「問題文を読んだあと、文を式に直す直前」など、自分がそれまでしてきたことと、違うことをやり始めるまさにそのときを意味します。

私が受け持った多くのお子さんを見てきて分かったことは、上に書いた「タイミング」において、「合っているかどうかを確かめないこと」「そもそも確かめ方を知らないこと」が原因で、「見直しができていない状態」が作られてしまっているということです。

そのせいもあって、お子さんにはミスをした覚えなどなく、正解を出したつもりになっていることも多いです。

確かめ方を知らないということであれば、お子さんは「思い込みや勘違い」によって、間違った考え方を「正しいと思い込んでいる部分がある可能性」もあります。

お子さんが具体的に、どんなことを勘違いしてしまうのかについては、こちらでも解説してありますので、気になる方はぜひご一読下さい。

https://sugaku1bann.com/2021/10/31/misudewanakutisikibusokukanntigai/

ここからは具体的に、その「タイミング」がどこにあるのかについて述べます。

見直しのタイミング１「問題文を振り返るとき 」

まず一つ目は、問題文を読んだあと、「どんな条件があったのかを振り返るとき」です。

そもそも振り返ることをしないというお子さんは、今からすぐに「問題文を振り返る」という癖をつけていきたいところです。

その条件を「自分勝手な思い込みで解釈していないかどうか」を確かめることが、見直しとして大切になってきます。

この場合の「見直し」とは何か「１本８０円のえんぴつを５本買えるお金で、同じ金額のボールペンを４本買いました。ボールペン１本の値段はいくらですか。」という文章問題を例としてお話していきます。

この問題文を読み、「自分勝手な思い込みで解釈していないかどうか」 を確かめるとは、「同じ金額のボールペン」という文言が出てきたことを振り返り、その文言は「ボールペンとえんぴつが同じ金額なのではなく、ボールペンが全て同じ金額である」という風に読むことが、正しかったかどうかを判断することなどにあたります。

算数・数学の問題文を読むときは、文法知識だけではなく、「算数・数学の問題文の読み方」を思い出した上で、どの数値とどの言葉が結びついているのかを判断します。

そうした判断をしていくことが、自分勝手な解釈をせずに問題文を読むことであると言えます。

しかし、そもそも「算数・数学の問題文の読み方」を知らないということであれば、また後でも書きますが「基本的な例題」を学ぶプロセスにおいて、問題の解き方だけではなく「問題文の読み方」も同時に、知識として習得していく必要があります。

動画でも解説しております。

https://youtu.be/8yVYZwTnghE

見直しのタイミング２「問題文の条件を図として描き表すとき」

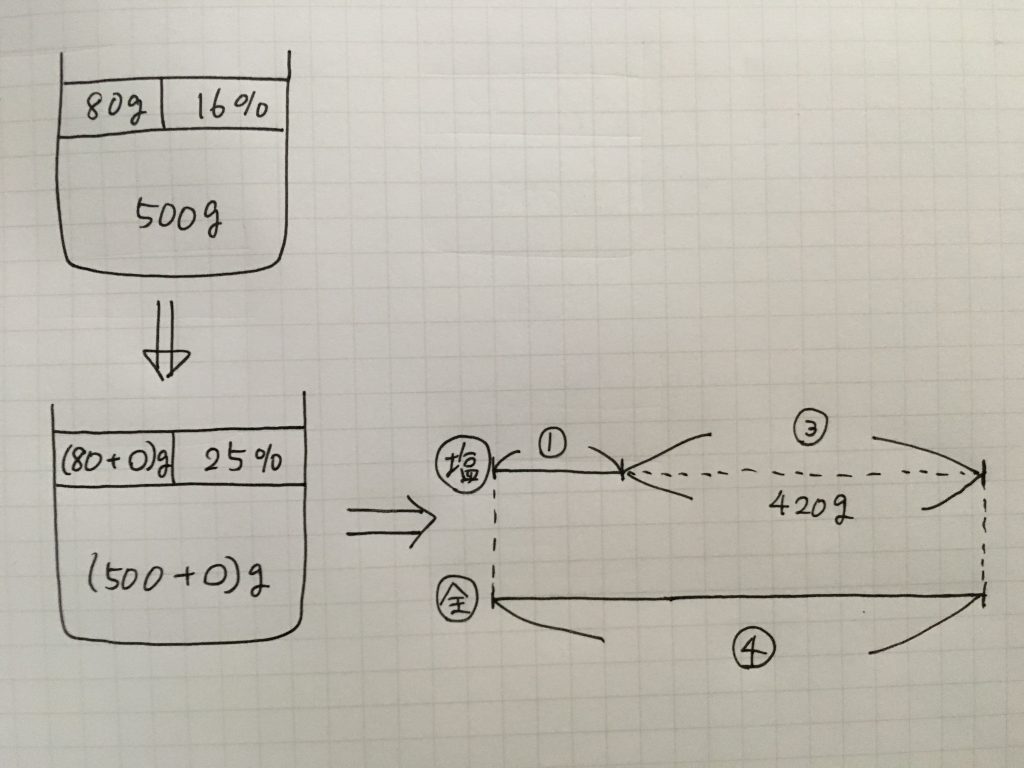
問題文を読み、条件がどんなものかを把握できた (かもしれない) とします。

本当に把握できたかどうかを、図に描くことで確かめられる場面があります。

中学受験の算数だと、文章問題であっても、「線分図」や「面積図」などを用いて、問題文を図に表すとどうなるかを考える場面があります。

そのときに、「自分が描いた図は、問題文を再現しているかどうか」を確かめることが大切です。

「図の中のここからここの長さは、問題文のこの量のことを言っているから、この図全体はあの量のことを指している」といった具合に、「合っているという明確な理由」を図と共に答えられるかどうかが、見直しをすることにつながります。

動画でも解説しております。

https://youtu.be/RCrAC_Ow740

見直しのタイミング３「立式するとき 」

問題文にある条件から、直接式を立てられる場合もあれば、一旦図に直してから式を立てる場合もあります。

算数・中学数学の場合は特に、「何かと何かが等しいことを表す関係式を作ること」が「立式する」ということになります。

立式した際には必ず、作った式が問題文の文章や自分が描いた図を、再現したものになっているかどうかを確かめることが大切です。

一見すると別のものがイコールで結ばれるという視点

立式の際に意識しておきたいことは、「一見すると別のものが、イコールの関係で結ばれること」が、正しいのかどうかを確かめる視点です。

上に書いた視点は特に、以下のような速さの問題で必要になります。

例題　「池にそって１周3600mの道がある。この道の上のある地点Ｐを、Ａ、Ｂ２人が同時に出発し、ＡはＢの３倍の速さで歩くものとする。同じ向きに歩いたら30分ごとにＡはＢを追い越した。Ａの速さは毎分何ｍか。」

中学受験の算数では、「ＡさんもＢさんも同じ時間 (この場合だと30分) だけ歩いているので、２人の速さの比が、２人が歩いた距離の比と等しくなる」という考え方を使って解くことになります。

ただ、「一見すると別のものが、イコールの関係で結ばれることが正しいかどうかを確かめる」という視点を持って立式する場面は、主に中学以降の数学で出てくるので、ここでは中学の数学における方程式の考え方に沿って、なぜこうした視点が必要になってくるのかについて、少しお話していきます。

上の例題を解く際にはまず、「求めるべきものを文字で置く」という考え方が必要になります。

ですので、この考え方に沿って立式することを考えると、まずはＡさんの速さをｘなどと置くことになります。

すると、Ｂさんの速さは「ｘ/３」となります。

問題文を振り返ると、「同じ向きに歩いたら30分ごとにAはBを追い越した」とあるので、この文章は「AさんとBさんが同時に歩き出したら、30分後にはAさんはBさんよりも１周分多く歩いている」という文言に言い換えられます。

ここでもやはり、「問題文を振り返り、文章を自分勝手に解釈していないかどうか」を確かめる場面が出てきます。

この場面で、正しい解釈ができていることに納得できたら、立式することになります。

具体的にこの例題においては、「Ａさんが速さｘで30分間歩いた距離」から「Ｂさんが速さ (ｘ/３) で30分間歩いた距離」を引いたものが「池のまわり１周分」となることを、式として表現します。

これはまさに、「Aさんが歩いた距離とBさんが歩いた距離の差」と「池のまわり１周分」という両者が、「一見すると別のもの」ではあるものの、ここでは「同じもの」とみなしているのです。

つまり30×Ⅹ−30×(Ⅹ/３)＝3600となりますが、実はこの式を作るタイミングにおいて、「一見すると別のものがイコールの関係で結ばれること」が、正しいかどうかを確かめる視点が大切になります。

この視点が大切だと思った理由

問題文を読み、一見すると別のものがイコールの関係にあるということに対して、それが正しいかどうかを確かめる視点が大切だと思ったのには、明確な理由があります。

というのも、上に書いた速さの問題で、私からお子さんに

「30×Ⅹ−30×(Ⅹ/３)がいくつになる？」

と聞いたときに、あるお子さんが「3600」とは、すぐに答えられないということがあったからです。

この問題について考えていたとき、私からそのお子さんに

「Ａさんの速さは？」「何分歩いたの？」

と聞いてみたところ、お子さんは「毎分Ⅹｍ」、「30分間」と答えることもできたのですが、その次からこんな会話がありました。

私「Ａさんが歩いた距離は？」

生徒さん「30×Ⅹ」

私「そうだね、Ｂさんが歩いた距離は？」

生徒さん「え？30×(Ⅹ/３)」

私「そうそう、ＡさんとＢさん比べて、どっちの方が長く歩いている？」

生徒さん「・・・、Aさん？」

私「そうだね。じゃあ、Aさんが歩いた距離から、Bさんが歩いた距離を引くとどうなる？」

生徒さん「30Ⅹ−30(Ⅹ/３)？」

私「そうそう、それがいくつになる？」

生徒さん「30X−10X＝20X」

私「OK。それが、具体的にいくつになる？」

生徒さん「具体的に？20Xじゃないの？」

私「うん、20Xが、具体的にどんな数と同じになるかな？」

生徒さん「・・・、え？」

私「もう一度、問題を振り返るね。今AさんとBさんは、どこ歩いている？」

生徒さん「池の周り」

私「そう。同じ向き？それとも反対向き？」

生徒さん「同じ向き」

私「ＯＫ。(描いた図も見ながら) AさんとBさんが同時に出発して、その後どうなったかな？」

生徒さん「30分後にAがBを追い越した」

私「AさんはBさんよりも、どれだけ多く歩いている？」

生徒さん「あ～、１周分多く歩いてるんだ。だから20X＝3600だ。」

私「そうなんだよね。どのタイミングで20Ｘが3600になるって分かった？」

生徒さん「図も見ながら、ＡとＢが歩くことを想像したら、１周多く歩いているって分かった。」

私「そうだったんだ。普段そういう風に想像しながら、何がどれと等しくなるのかについて、確かめたりしてる？」

生徒さん「う～ん、あんまりしてない。この問題も、問題文をただ読んでるだけじゃ、こんな式が立つこと分からない。」

この視点を身に付けるために必要なこと

このお子さんは「２人の距離の差が、この問題においては池のまわりの長さ１周分と等しくなる」という状況について、図を描いてみて、「AさんとBさんが動くところ」を思い浮かべることで理解できてきました。

しかし、更にお話を聴くと、普段図を描くことがあっても、「何がどれと等しくなるのか」という疑問を持ち、それに自分で答えることができていないということだったのです。

この場合はそういったことも原因で、お子さんは「20X＝3600」という式を、すぐには作ることができなかったと考えられます。

だからこそ、上に出てきた速さの問題の類題に対しては、「一見すると別のものがイコールで結ばれることが正しいかどうかを確かめる視点」も、まだこの時点ではなかったと考えられるのです。

「問題文の読み方を知らない」ということとも関係してきますが、このお子さんは「AはBよりも、１周分多く歩いたって、直接書いてくれれば良いのに・・・」と後から言っていました。

このような場合は、類題をまた繰り返し解きながら、「問題文の読み方・言い換え方」「言い換えたことを、式として表現するとどうなるのか」を習得していくことが課題となります。

その課題を乗り越えるプロセスにおいて、「立式したものが正しいのかどうかを確かめる視点」を身につけていくのです。

まとめると、立式をして「一見別のものをイコールで結んでいること」を表している場合には、「なぜそれとこれがイコールなのか」を、問題文を振り返り、その疑問に対して自分で答を与えられるようにすることが大切です。

具体的には、問題文の条件や自分が描いた図を振り返り、「この文章のここからここまでが、この量と等しい」といった考えなどを、アウトプットできることが大切です。

そのことが、「立式をする場面における見直し」につながります。

見直しのタイミング４「式変形をするとき」

問題文を読み、どんな条件があったのかを振り返り、条件を自分勝手に解釈していないかどうかを、図に描くことなどを通して確かめてから立式し、「本当に左の式と右の式はイコールか？」という疑問に対して、自分で納得できる答を与えることができたら、その式を計算していきます。

一言に「計算する」と言っても、大きく分けてそれが「式変形」なのか、「逆算 (方程式を解くこと) 」なのかで、「何のためにその計算をするのか？」といった目的や、式中のどの部分に注目するのかが異なります。

すなわち、式を計算していく上では、「イコールで式を結ぶ以上、左の式と右の式が同じかどうか」を確かめることはもちろん、その「目的」と「計算式の目のつけどころ」を振り返ることも、見直しのポイントに含まれます。

例えば考えやすい例として、小学生の算数の問題で、四角形のまわりの長さの問題があります。

「たての長さが〇ｃｍ、横の長さが５ｃｍ、四角形のまわりの長さが３６ｃｍのとき、たての長さは？」

という問題があったとき、図を描いて立式して、「(〇＋５)×２＝３６」といった式が出てきたとします。

このとき、上に書いた「(〇＋５)×２＝３６」という式を「計算する」とはどういうことなのかについて、「式変形」と「逆算 (方程式を解く) 」という側面から、その意味を明確にしていきます。

以下では小学算数で出てくる「逆算すること」と、中学数学で出てくる「方程式を解くこと」を、まとめて「方程式を解くこと」ということにします。

式変形における見直しポイント

まずここでは、「式変形」についてお話します。

「式変形」とは「方程式を解くためにする行動」ということになります。

高校以降の数学になってくると、不等式を解くことを目的として行う場面が増えます。

上に書いた「(〇＋５)×２＝３６」の例だと

(〇＋５)×２＝〇×２＋５×２

という具合に、「もともと作った式の形を変える」ことが式変形です。

そして、大事なのは「何のためにその式変形をするのか？」という疑問を持つこと、あるいはそれに答えることです。

お子さんがもし、上の問題に対して、同じ式変形をしたとします。

確かに、上の黒い太字の式変形は、合ってはいます。

もちろん、イコールで式を結んでいる以上、合っているかどうかを確かめる必要があります。

しかし、お子さんに「何のためにその式変形をするのか？」と聞いたときに、うまく答えられないといった状況があるのであれば、「式変形は合っていても、目的が違っている」という構図が生まれていることが考えられます。

式変形をするときには、そのやり方だけではなく、「式変形をする目的」が合っているかどうかも確かめる必要性があります。

そのことが「計算途中、特に式変形における見直し」の一つです。

上に書いた水色の式変形において、「〇の値 (たての長さ) を求めるために、式変形をする」というのであれば、式変形をする目的は理解できていると言えます。

見直しのタイミング５「方程式を解くとき」

次に、「方程式を解く」という側面から、計算途中での見直しポイントを考えていきます。

そのために、上ではあえて「(〇＋５)×２＝〇×２＋５×２」という一見遠回りな式を出しました。

上の「」内の式は、「式変形をしても、左の式と右の式は同じ」ということを表しています。

そもそもしたいことは何かというと、「〇の値 (たての長さ) 」を求めることであり、それはつまり「(〇＋５)×２＝３６」という式において、〇の中にどんな数が入るのかを答えることです。

〇×２＋５×２＝３６という式をモデルとして、方程式を解くプロセスにおいては、どんな見直しポイントがあるのかについて述べます。

と言っても、大事なのはたった二点です。

方程式を解く際の見直しポイント

まず一つ目は「壊してはいけない塊 (かたまり) 」が何かを確かめることです。

壊してはいけない塊とは「×や÷の記号でつながれた数 (または文字) 同士」のことを言います。

上に書いた式でいうと「〇×２」と「５×２」のことです。

どの数とどの数が「×の記号」で結ばれているのかを見間違わないことなどが、見直しのポイントです。

もう一つの見直しポイントは、「その塊がいくつであれば良いのか」を確かめることです。

〇×２＋５×２＝３６という式では、「５×２＝１０」となることに加えて、「〇×２」がいくつであれば良いのかを考える場面があります。

ここで大事なのは、「〇×２」は、何か一つの数を表しているといった見方ができることです。

これまで「一つの塊」と言ってきましたが、それは具体的には「一つの数」です。

方程式を解く際、計算式の中にある「壊してはいけない塊」を見つけて、それを具体的に「一つの数」だと思うことが、認識の仕方としては大切です。

その「一つの数」が、具体的にいくつなのかを勘違いしていないかどうかを確かめることが、方程式における見直しポイントです。

見直しのタイミング６「自分は何を求めたのか」を振り返るとき

(〇＋５)×２＝３６ の例だと、塊に注目できて、その塊がいくつになるのかも分かった上で、〇＝１３ と、答を求められるのであれば問題はありません。

〇がもともと何を表すのかも、分かっているのであれば、「自分は何を求めたのか？」も理解できます。

その場合は、「自分は何を求めたのか？」を振り返ることが、どこかしらでできていると言えますが、私が見てきたお子さんの中には、「自分はこの計算をして、何を求めたのか？」を振り返る場面がないというお子さんもいました。

(〇＋５)＝１８になれば良いということが分かっているにもかかわらず、そのまま答を１８と書いてしまうタイプのお子さんなどがそうです。

他にも、立体の表面積を求めるときなどは、「この面の面積が〇〇ｃｍ＾２」というように、自分はいま「どこの何を計算で求めているのか」を振り返る場面も、見直しのタイミングの一つです。

計算が済んだら、「それはいま何を求めたのか？」を気にとめておくことが大切です。

分野ごとに異なる見直しのタイミング７選

これまで、見直しをかける６つのタイミングについてお話をしてきました。

この６つのタイミングというのは、どんな分野の問題を解く際にも共通して現れます。

ならば当然、分野ごとに細かく見ていったときに、「その分野特有の見直し」というものもあります。

ここでは簡単に、どんな分野の問題で、どういった見直しのタイミングが存在するのかについて、見ていきます。

「単位を換えるとき」以外は、中学の数学でもあてはまるものが多いので、中学生のお子さんがいらっしゃる方は、ご一読頂けると幸いです。

数・ものの個数を数え上げるとき

数の性質を問う問題では特に、「３の倍数は何個あるか」といった問題のように、「具体的に数え上げてから一般的な結果を出す」という場面があるものがあります。

規則性を見つける問題もそうですが、「数やものの個数を数え上げるとき」に、数え間違いなどが起きていないかどうかを確かめることがあります。

底辺と高さを設定するとき

意外にも多いのが「底辺と高さ」の関係を知らない、あるいは忘れているというお子さんです。

問題で図形が与えられたときに、見方を変えるなどして、自分で底辺と高さを設定してから面積を求める問題があります。

そのときに、「底辺と高さ (だと思ったもの) が、９０°で交差しているかどうか」を確かめることが、見直しのポイントです。

どこの面を下に置くかを決めるとき

特に柱体の体積を求めるとき、「その面を下に置くことで、太さが変わらない柱が立ったことになるのか？」を確かめてから、「底面積×高さ」を計算することになります。

上の「」内に書いたことを確かめることが、立体 (特に柱体) の体積を求める際には大切です。

展開図ともとの立体を比較するとき

展開図を描いて何をするかのというと、展開図の中に描かれている辺や頂点は、どこの辺と頂点と重なるのか？を確かめるのです。

それはつまり、「その辺と辺 (または頂点と頂点) を重ねることで、もとの立体を再現するのか？」を考えるということです。

展開図を描く限り、このようなことは、必ず振り返る必要があります。

場合分けをするとき

「カードを並べて、こんな場合が何通りできるのか？」を考えるタイプの問題では、場合分けをして「本当にそれ以上あてはまる場合がないのか？」を考える場面があります。

例えば「０から４までの数が書かれたカードを３枚並べて、できた数が３の倍数になる場合」を考えるとき、３の倍数になる場合を書き出してみて、「本当にこれ以上あてはまる場合がないのか」「かぶっている場合がないか」を確かめることが見直しです。

単位を換えるとき

速さや水の量を計算する問題では「分速を時速に直すこと」や「リットルをｃｍ＾３に直す」場面があります。

これらも立派な見直しのタイミングに含まれます。

特にリットルからｃｍ＾３への変換は、単位の関係を覚えていないと問題が解けないので、覚えるのが苦手というお子さんは、繰り返し基本問題を解くなどして、対策をしていくことが大切です。

グラフを見て問題を解くとき

グラフの問題は、算数では「速さ・水量・図形が動く問題」などで共通して出てきます。

グラフの問題を解く際に共通するのは、「問題文に書いてあることが、グラフとしてどう表現されているのか」を見抜くことです。

ここに、見直しのタイミングが潜んでいます。

例えば速さの問題では、「進んでから何分休んだ」という問題文があったときに、その問題文がグラフでは「斜めの線ではなくまっすぐな線になっている部分」として表されています。

そのときに「それが進みはじめて何分後のことなのか」を、問題文を振り返りながら確かめることや、グラフに数を書き込むときに、書き間違いがないかを確かめることなどが、見直しをするということです。

まとめ

一言に「見直しをする」と言っても、ここでお話してきたように、「いつ」「どこで」「何をするのか」という視点を持って、改めて見直しとは何かを考えたとき、「見直しのタイミング」というものがあることが分かります。

そして、「なぜそのタイミングで見直しをするのか」を考えたときに、「このことを確かめたいがために、ここに見直しのタイミングがある」という答があるように、見直しの目的というものが同時にあることも分かります。

この記事では、具体的な見直しのタイミングについて書いてきましたが、また今度別の記事で、「そのタイミングにおいて何をすることが見直しをすることなのか」「何ができたら見直しができたことになるのか」について書いていきたいと思います。