こんにちは。算数・数学専門家庭教師の鈴木です。
今日は「予習シリーズの4年下」で体積と表面積を勉強するお子さんが、ぜひ押さえておいてほしいポイントについて解説します。
柱体の単元においては「体積の求め方がよく分からない」「表面積を間違えてしまう」などなど、4年生にとっては難しく感じるところも多くあるかもしれません。
私のところの生徒さんも、はじめは表面積が何なのか分からないといった様子でしたが、ここで解説していくことを意識することで、理解できてきました。
ですのでこの記事は、中学受験を目指す小学4年生が体積と表面積の求め方を理解する上で、非常に参考になるものだと思います。
円柱と三角柱を組み合わせた立体の問題がこちら
予習シリーズにはさまざまな練習問題が載っていますが、今日はこのような問題を解説します。

【体積を求めるときのポイント1】底面を決める
柱体の体積を求めるときに大事なのは「どの面が底面になるのかを考えること」です。
ですので、まずは立体を床に置くことを考えたときに「床にくっつく面」を考えて下さい。
大事なのは「床にくっつく面」と「立体の真上から見える面」が全く同じ形になるとき、床にくっつく面を「底面」と言います。
上の問題ではすでに「床にくっつく面」と「真上から見える面」が全く同じになっていますよね。
この問題の場合、底面は「三角形と円の半分」からできているので、まずはその面積を求めます。
【体積を求めるときのポイント2】体積=「底面積×高さ」
柱体の体積は「底面積×1」のものが「高さの分だけ積まれてできる大きさ」という考えのもとで求められます。
この考え方こそ、体積の基本です。
このような考え方を経て
底面積=6×4÷2+3×3×3.14÷2=26.13
体積=26.13×8=209.04
答は209.04㎝^3になります。

【表面積を求めるときのポイント1】展開図を描く
「表面積を求めるのが苦手!」というお子さんは、ほぼ共通して「展開図を描いていない!」という事実があります。
後でも書きますが、表面積とは「その立体を形作る全ての面の面積の和」です。
ですので、表面積を求める際には「この立体はどんな面からできているのだろう」と考えることは必須です。
このような理由から、必ず展開図を描いて下さい。
もしお子さんが「展開図が描けない!」という状況であれば、解説を見ながら「展開図を写す練習」から始めるのも一つの手です。

【表面積を求めるときのポイント2】面の数を数える
展開図を描いたら、次はその図を見て「どんな図形からできているか」「どんな図形が何面あるのか」を調べます。
この問題の場合だと、以下のように「長方形が3面」「三角形が2面」「半円が2面」あることが分かります。
合計7面あるということですね。
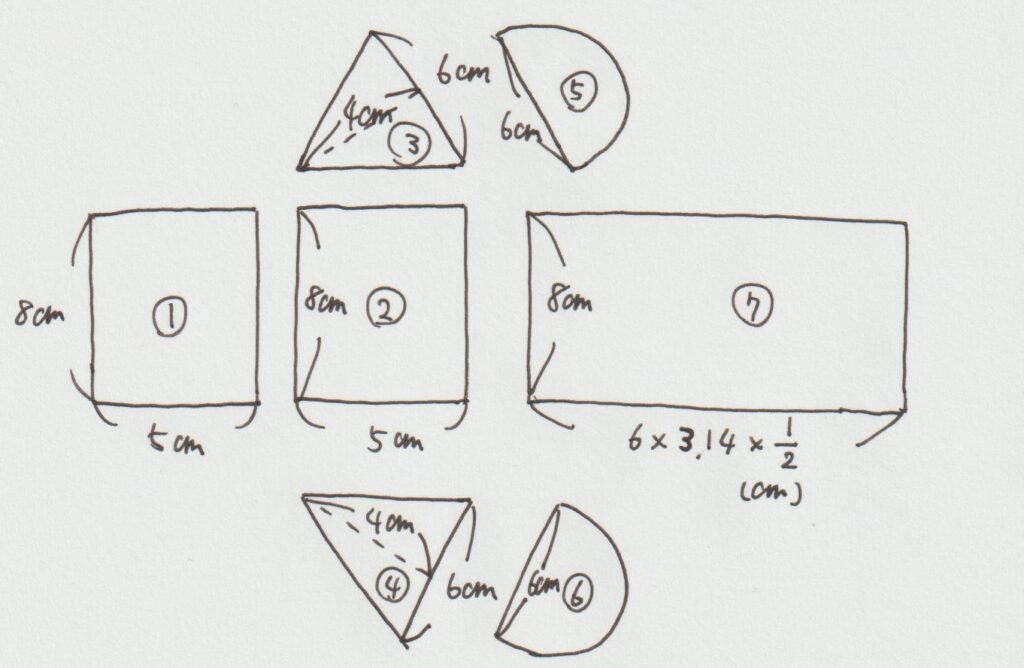
【表面積を求めるときのポイント3】それぞれの面積を出す
「どんな図形からできているのか」が分かったら、各面の面積を求めます。
このときに大事なのは、展開図を描いた際に「どの辺とどの辺がくっつくのか」を考えることで「この辺の長さは〇〇㎝になる!」と自信を持って言えることです。
展開図を組み立てたときのことも考えて「辺の長さを見間違っていないか」「書き間違いはないか」を確かめながら、面積を計算することが大事です。

【表面積を求めるときのポイント4】全ての面積を足す
大事なことですので何度もお伝えしますが、表面積とは「その立体を形作る全ての面の面積の和」のことです。
表面積を求める際には、面の数を数えたりしなければいけないことから「この公式で必ず答が出る」という裏技のようなものはありません。
ここがお子さんにとって「難しいと感じる部分」の一つでもあります。
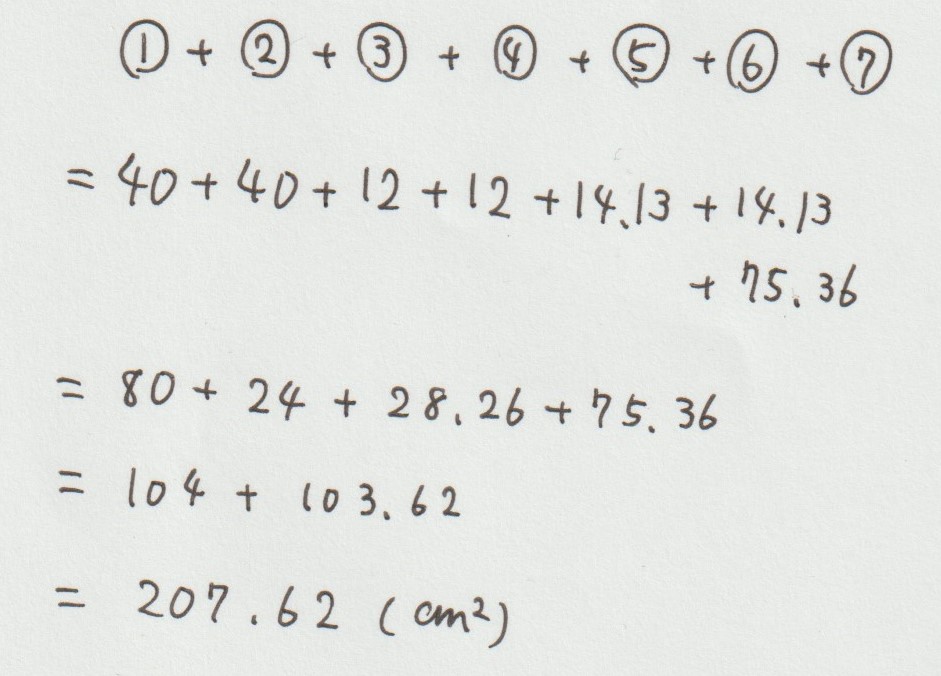
表面積を出すときに大事なのは「展開図を描くこと」
表面積を出すときに一番何が大事かというと、間違いなく「展開図を描くこと」です。
過去に表面積を出すことに苦手意識があった生徒さんもいましたが、展開図を描けるようになったことで、正解を出せるようになった事例も多いです。
展開図を描き「組み立てたところまで想像すること」ができると、解ける問題も増えていきます!
まとめ
体積・表面積は本来であれば小学5、6年で習うことですので、今できなくても「そのうちできるようになる!」という気持ちを持って学ぶことも大事です。
そのためにも、もう一度以下に書くことを思い出して、ここで出てきた類題などを解いてみて下さい。
・底面を決める
・体積=「底面積×高さ」
・展開図を描く
・全ての面を数える
