「弁償算って難しい…」「どうやって解けばいいのか分からない」と感じていませんか?
この記事では弁償算の基本的な考え方から、応用問題の解き方まで、算数・数学の家庭教師歴15年のプロ家庭教師が解説します。
具体的には、弁償算の基本、解法のポイント、そしてつるかめ算との関係まで、丁寧に説明しています。
読むことで、弁償算の理解が深まり、中学受験の算数に自信が持てるようになりますので、ぜひ最後までお読みください。
弁償算とは?基本例題とつるかめ算との関係
「弁償算」は中学受験を目指すお子さんが小学4年生の段階で、つるかめ算と共に習うことになっています。
また今度つるかめ算についての記事も書こうと思うのですが、つるかめ算も弁償算も、本当は「面積図」というものを描いて解きます。
「本当は・・・」としたのは、実は今あまり面積図を習わないことも多いと聞くからです。
この記事では、まずは基本的な問題を題材として、つるかめ算との関係から解説していきます。
弁償算の基本例題
弁償算では、以下のような問題が基本的です。
| 「例題1」コップを200個運ぶ仕事があります。1個運ぶごとに30円をもらえます。しかし、コップを割ってしまうと、30円をもらえないだけでなく、1個につき90円をはらうことになります。花子さんはこの仕事で5280円をもらいました。割らずに運んだコップは何個ですか。 |
つるかめ算との関係
つるかめ算では「全て~だったら・・・」と仮定して解く人も多いですよね。
その意味では弁償算の問題も、例えば上のような問題であれば「全部わらずに運べたら・・・」と考えて解くことができます。
弁償算の解法ステップと面積図
ここからは「例題1」をどのようにして解くのかについて解説します。
「すべてわらずに運んだ」と仮定して考える
まずつるかめ算でも出てくることですが「全部わらなかった」と仮定してみましょう。
そうすると、本来は「200×30=6000 (円) 」もらえるはずだったわけです。
しかし、実際は5280円ですので、何個かわってしまったことになります。
大事なのは「弁償するお金」は「もらった報酬分の中から出す」ということです。
この考え方があるからこそ「もらう予定だった金額よりも少なくもらう」ということになります。
報酬と弁償額の関係を面積図で表す
この「何個かわってしまった」という状況を「面積図」で表します。
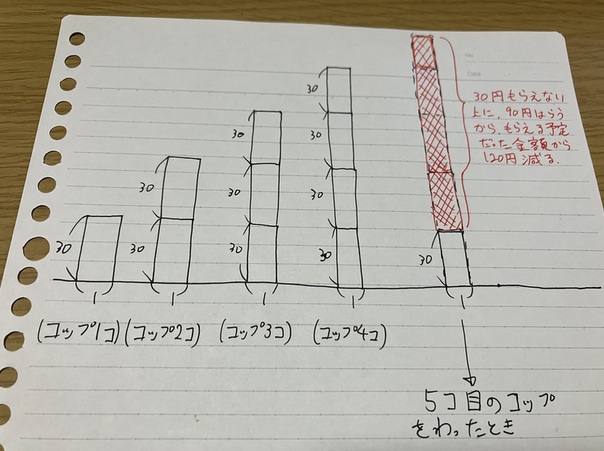
正確には「面積図」とは言わないかもしれないのですが、上の図では、例えば4個のコップをわらずに運んだのに、5個目でわってしまったときにもらえる金額を図で表しています。
もう一度言いますが、弁償する金額は「もらった報酬分からはらう」ということになります。
このことから、上の図における例では、4個わらずに1個わってしまったら、もらえる金額は「たった30円」です。
なぜこのようなことが起きるのか、以下で説明しますね。
弁償算の計算テクニック
上の例では、もし「5個全てわらずに運ぶ」ということができたら、もらえる報酬は「30×5=150 (円) 」だったわけです。
ところが1個わってしまっているので「もらえるはずの30円」と「弁償代の90円」を足した120円分損してしまっていることが、図から分かります。
つまり、コップを1個わるごとに、本来もらえるはずだった金額分から「120円×(わったコップの数) 」だけ、実際にもらえる金額は減ることになるのです。
このことから、上のような例題では以下の式が成り立ちます。
「実際にもらえる金額」=「もらえるはずだった金額」-「(報酬)+(弁償代)」×「わったコップの数」
この式を使うと、上の例題は
5280=6000−120×「わったコップの数」
これを解くと、わったコップの数は6個となります。
まとめ
いかがだったでしょうか。
弁償算は式の作り方が難しい部分もありますが、上のような図を描くと分かりやすくなります。
ぜひこの記事も参考に、勉強を進めてみて下さいね。

中学受験の算数が苦手という方に向けて、家庭教師指導を行っております。
個別指導歴15年のプロ家庭教師の鈴木が、算数のお悩みを解決します。
「成績を上げたいけれどうまくいかない」「家庭教師指導をお願いしたい」などのご相談事がありましたら、以下のフォームよりお問合わせ下さいませ。
